题目内容
某中学举行了一次“环保知识竞赛”活动.为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计.按照 ,
,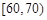 ,
, ,
,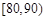 ,
,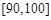 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在 ,
,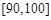 的数据).
的数据).
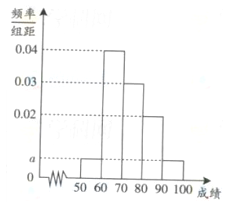
频率分布直方图 茎叶图
(1)求样本容量n和频率分布直方图中x、y的值;
(2)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学到市政广场参加环保知识宣传的志愿者活动,求所抽取的2名同学来自不同组的概率.
(1)0.004,0.030;(2)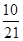 .
.
解析试题分析:(1)由频率分布直方图可求出分数在50到60的频率,由茎叶图可得出分数在50到60的人数,
由此可得样本容量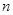 .又由茎叶图可得分数在90到100的人数,从而求得
.又由茎叶图可得分数在90到100的人数,从而求得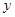 .这样除了60到70分这一组之外,其余各组的频率都知道了,也就可以求出
.这样除了60到70分这一组之外,其余各组的频率都知道了,也就可以求出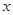 的值了.(2)由(1)可知,分数在[80,90)有5人,分数在[90,100)有2人,共7人.将这7人用不同字母表示出来,然后将取出2人所有基本事件(即可能出现的结果)一一列出,数出来自不同组的基本事件事件的个数,由古典概型的概率公式即得所求概率.
的值了.(2)由(1)可知,分数在[80,90)有5人,分数在[90,100)有2人,共7人.将这7人用不同字母表示出来,然后将取出2人所有基本事件(即可能出现的结果)一一列出,数出来自不同组的基本事件事件的个数,由古典概型的概率公式即得所求概率.
(1)由题意可知,样本容量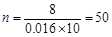
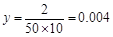
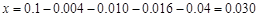 .
.
(2)由题意可知,分数在[80,90)有5人,分别记为a,b,c,d,e,分数在[90,100)有2人,分别记为F,G.从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学有如下种情形:(a,b),(a,c),(a,d),(a,e),(a,F),(a,G),(b,c),(b,d),(b,e),(b,F),(b,G),(c,d),(c,e),(c,F),(c,G),(d,e),(d,F),(d,G),(e,F),(e,G),(F,G),共有21个基本事件;其中符合“抽取的2名同学来自不同组”的基本事件有(a,F),(a,G),(b,F),(b,G),(c,F),(c,G),(d,F),(d,G),(e,F),(e,G),共10个,所以抽取的2名同学来自不同组的概率 .
.
考点:1、用样本估计总体,2、古典概率.

某普通高中共有教师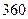 人,分为三个批次参加研修培训,在三个批次中男、女教师人数如下表所示:
人,分为三个批次参加研修培训,在三个批次中男、女教师人数如下表所示:
| | 第一批次 | 第二批次 | 第三批次 |
| 女教师 | 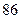 |  |  |
| 男教师 | 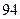 | 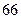 |  |
已知在全体教师中随机抽取1名,抽到第二、三批次中女教师的概率分别是
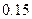 、
、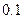 .
.(1)求
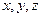 的值;
的值;(2)为了调查研修效果,现从三个批次中按
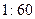 的比例抽取教师进行问卷调查,三个批次被选取的人数分别是多少?
的比例抽取教师进行问卷调查,三个批次被选取的人数分别是多少?(3)若从(2)中选取的教师中随机选出两名教师进行访谈,求参加访谈的两名教师“分别来自两个批次”的概率.
某种产品的广告费支出x与销售额 (单位:百万元)之间有如下对应数据:
(单位:百万元)之间有如下对应数据:
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 50 | 60 | 70 |
(1)请画出上表数据的散点图.
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
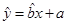 .
.(3)经计算,相关指数
 ,你可得到什么结论?
,你可得到什么结论?(参考数值:2×30+4×40+5×50+6×60+8×70==1390)
为预防X病毒爆发,某生物技术公司研制出一种X病毒疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司选定2000个样本分成三组,测试结果如下表:
| 分组 |  组 组 | 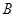 组 组 |  组 组 |
| 疫苗有效 | 673 | 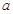 | 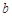 |
| 疫苗无效 | 77 | 90 | 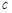 |
已知在全体样本中随机抽取1个,抽到
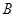 组疫苗有效的概率是0.33.
组疫苗有效的概率是0.33.(1)现用分层抽样的方法在全体样本中抽取360个测试结果,应在
 组抽取样本多少个?
组抽取样本多少个?(2)已知
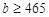 ,
,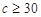 ,求通过测试的概率.
,求通过测试的概率. 
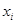 (年)与所支出的维修费
(年)与所支出的维修费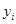 (万元)的数据资料算得如下结果,
(万元)的数据资料算得如下结果,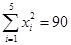 ,
,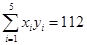 ,
,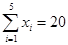 ,
,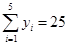 .
.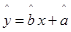 ;
;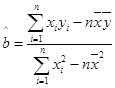 ,
,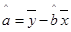 ,其中
,其中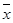 ,
, 为样本平均值.)
为样本平均值.)