题目内容
某班主任对全班50名学生的积极性和对待班级工作的态度进行了调查，
统计数据如下表所示：
| | 积极参加班级工作 | 不太积极参加班级工作 | 合计 |
| 学习积极性高 | 18 | 7 | 25 |
| 学习积极性一般 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
试运用独立性检验的思想方法分析：学生的学习积极性与对待班级的态度是否有关系？
|
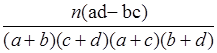
| P(K2≥k0 ) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
99.9％的把握认为学生的学习积极性与对待班级工作的态度有关系
解析试题分析：
首先根据列联表可知,
，从而根据随机变量
的公式，可得其值.根据所得的的值,与表中的数据进行比较,从而确定临界值.最后根据:如果
,就以
的把握认为相关量有关,否则无关.判断结果即可.
试题解析：由题意知：,
所以
可得
因为
所以可以有99.9％的把握认为学生的学习积极性与对待班级工作的态度有关系。
考点：独立性检验的基本思想.
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
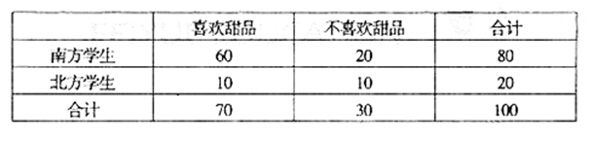
巴西世界杯足球赛正在如火如荼进行.某人为了了解我校学生“通过电视收看世界杯”是否与性别有关,从全校学生中随机抽取30名学生进行了问卷调查,得到了如下列联表:
| | 男生 | 女生 | 合计 |
| 收看 | 10 | | |
| 不收看 | | 8 | |
| 合计 | | | 30 |
已知在这30名同学中随机抽取1人，抽到“通过电视收看世界杯”的学生的概率是
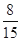.(I)请将上面的列联表补充完整,并据此资料分析“通过电视收看世界杯”与性别是否有关?
(II)若从这30名同学中的男同学中随机抽取2人参加一活动,记“通过电视收看世界杯”的人数为X,求X的分布列和均值.
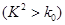  | 0.100 | 0.050 | 0.010 |
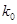 | 2.706 | 3.841 | 6.635 |
(参考公式：
， 
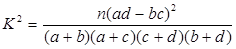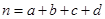) 某工厂为了对新研发的一种产品进行合理定价，将该产品按事先拟定的价格进行试销，得到如下数据:
单价 （元） | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量 （件） | 90 | 84 | 83 | 80 | 75 | 68 |
（1）根据上表可得回归直线方程
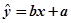中的
，据此模型预报单价为10元时的销量为多少件?（2）预计在今后的销售中，销量与单价仍然服从（1）中的关系，且该产品的成本是4元/件，为使工厂获得最大利润，该产品的单价应定为多少元？（利润=销售收入
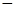成本） 
与销售额
（单位：百万元）之间有如下对应数据：
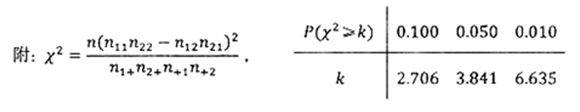
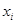（年）与所支出的维修费
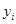（万元）的数据资料算得如下结果，
，
，
，
.
；
，
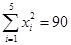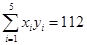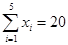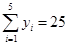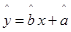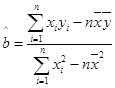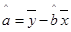，其中
，
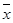为样本平均值.)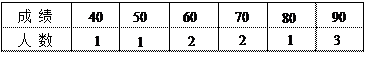
）.
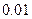