题目内容

8．已知函数f（x）=ex-2+a有零点，则实数a的取值范围为a＜2．

分析 利用函数的单调性求解函数函数f（x）=ex-2的最值，然后推出a的范围即可．

解答 解：函数g（x）=ex-2函数是增函数，g（x）＞-2，
函数f（x）=ex-2+a有零点，可得a=2-ex，可得a＜2．
故答案为：a＜2．

点评 本题考查函数的零点，函数的最值的应用，考查转化思想以及计算能力．

练习册系列答案
相关题目
1．定义区间[x1，x2]的长度为x2-x1（x2＞x1）单调递增），函数$f（x）=\frac{{（{a^2}+a）x-1}}{{{a^2}x}}$（a∈R，a≠0）的定义域与值域都是[m，n]（n＞m），则区间[m，n]取最大长度时实数a的值（　　）
A．$\frac{{2\sqrt{3}}}{3}$B．-3C．1D．3
19．在底面是菱形的四棱锥P-ABCD中，PA⊥底面ABCD，点E为棱PB的中点，点F在棱AD上，平面CEF与PA交于点K，且PA=AB=3，AF=2，则$\frac{AK}{PK}$等于（　　）
A．$\frac{2}{3}$B．$\frac{3}{5}$C．$\frac{4}{7}$D．$\frac{5}{9}$
16．某公司要招聘甲、乙两类员工共150人，该公司员工的工资由基础工资组成．其中甲、乙两类员工每人每月的基础工资分别为2千元和3千元，甲类员工每月的人均绩效工资与公司月利润成正比，比例系数为a（a＞0），乙类员工每月的绩效工资与公司月利润的平方成正比，比例系数为b（b＞0）．
（Ⅰ）若要求甲类员工的人数不超过乙类员工人数的2倍，问甲、乙两类员工各招聘多少人时，公司每月所付基础工资总额最少？
（Ⅱ）若该公司每月的利润为x（x＞0）千元，记甲、乙两类员工该月人均工资分别为w甲千元和w乙千元，试比较w甲和w乙的大小．（月工资=月基础工资+月绩效工资）
3．在△ABC中，∠A的角平分线交BC于点D，且AD=1，边BC上的高AH=$\frac{1}{2}$，△ABD的面积是△ACD的面积的2倍，则BC=$\frac{\sqrt{3}}{2}$．
13．设ϕ（x）是定义在[m，n]上的函数，若存在r∈（m，n），使得ϕ（x）在[m，r]上单调递增，在[r，n]上单调递减，则称ϕ（x）为[m，n]上的F函数．
（1）已知$ϕ（x）=\frac{x+a}{e^x}$为[1，2]上的F函数，求a的取值范围；
（2）设$ϕ（x）=px-（\frac{x^2}{2}+\frac{x^3}{3}+\frac{x^4}{4}+\frac{{p{x^5}}}{5}）$，其中p＞0，判断ϕ（x）是否为[0，p]上的F函数？
（3）已知ϕ（x）=（x2-x）（x2-x+t）为[m，n]上的F函数，求t的取值范围．
20．执行如图所示的程序框图，输出的S=（　　）
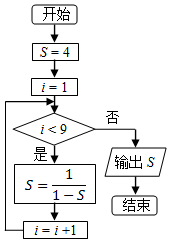
A．4B．$-\frac{1}{3}$C．$\frac{3}{4}$D．$\frac{1}{2}$
16．等差数列中{an}，a1=2，公差为d，则“d=4”是“a1，a2，a5成等比数列”的（　　）
A．充要条件B．充分非必要条件
C．必要非充分条件D．非充分非必要条件
15．直线l：kx+y+4=0（k∈R）是圆C：x2+y2+4x-4y+6=0的一条对称轴，过点A（0，k）作斜率为1的直线m，则直线m被圆C所截得的弦长为（　　）
A．$\frac{\sqrt{2}}{2}$B．$\sqrt{2}$C．$\sqrt{6}$D．2$\sqrt{6}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网