Question

【题目】已知函数

(1) 求函数的反函数；

(2)试问:函数的图象上是否存在关于坐标原点对称的点，若存在，求出这些点的坐标；若不存在，说明理由；

(3)若方程的三个实数根满足: ，且，求实数的值．

Answer 1

【答案】（1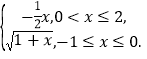）；（2）存在点关于原点对称；（3）.

【解析】试题分析：(1)根据分段函数的反函数的求法求出函数的反函数；

(2)设点是函数图象上关于原点对称的点，

则，即， 解方程求出，即可说明：函数图象上存在两点关于原点对称.

(3) 根据函数与函数的图象，可得

当时，，且.；

当时， ，于是，.

由，解得.，满足条件.因此，所求实数.

试题解析：(1)

当时，.

由，得，互换，可得.

当时，.

由，得，互换，可得.

(2) 答：函数图象上存在两点关于原点对称.

设点是函数图象上关于原点对称的点，

则，即，

解得舍去），且满足 .

因此，函数图象上存在点关于原点对称.

(3) 考察函数与函数的图象，可得

当时，有，原方程可化为，解得

，且由，得.

当时，有，原方程可化为，化简得

，解得(当时，).

于是，.

由，得，解得.

因为，故不符合题意，舍去；

，满足条件.因此，所求实数.