题目内容
若函数f（x）=
的定义域为R，则实数m的取值范围是______．
| mx2-6mx+m+8 |
依题意，当x∈R时，mx2-6mx+m+8≥0恒成立．
当m=0时，x∈R；
当m≠0时，
即
，解之得0＜m≤1．
故答案为0≤m≤1．
当m=0时，x∈R；
当m≠0时，
|
|
故答案为0≤m≤1．
练习册系列答案
怎样学好牛津英语系列答案
相关题目
怎样学好牛津英语系列答案
和圆x2+y2=n2相切，其中m，n∈N，0＜|m-n|≤1，若函数f（x）=mx+1-n的零点x∈（k，k+1）k∈Z，则k= ．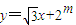
和圆x2+y2=n2相切，其中m，n∈N，0＜|m-n|≤1，若函数f（x）=mx+1-n的零点x∈（k，k+1）k∈Z，则k= ．