题目内容
若函数f(x)=mx+
在区间[0,1]单调递增,则m的取值范围为( )
| x |
分析:求导数f′(x),由f(x)在[0,1]上单调递增,得f′(x)≥0即m+
≥0在(0,1]上恒成立,分离出参数m后转化为函数最值解决即可.
| 1 | ||
2
|
解答:解:f′(x)=m+
,
因为f(x)在[0,1]上单调递增,
所以f′(x)≥0即m+
≥0在(0,1]上恒成立,也即m≥-
恒成立,
而-
在(0,1]上单调递增,所以-
≤-
,
故m≥-
,
故选A.
| 1 | ||
2
|
因为f(x)在[0,1]上单调递增,
所以f′(x)≥0即m+
| 1 | ||
2
|
| 1 | ||
2
|
而-
| 1 | ||
2
|
| 1 | ||
2
|
| 1 |
| 2 |
故m≥-
| 1 |
| 2 |
故选A.
点评:本题考查函数单调性的性质,考查导数与函数单调性的关系,考查转化思想,考查学生分析解决问题的能力.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 和圆x2+y2=n2相切,其中m,n∈N,0<|m-n|≤1,若函数f(x)=mx+1-n的零点x∈(k,k+1)k∈Z,则k= .
和圆x2+y2=n2相切,其中m,n∈N,0<|m-n|≤1,若函数f(x)=mx+1-n的零点x∈(k,k+1)k∈Z,则k= .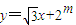 和圆x2+y2=n2相切,其中m,n∈N,0<|m-n|≤1,若函数f(x)=mx+1-n的零点x∈(k,k+1)k∈Z,则k= .
和圆x2+y2=n2相切,其中m,n∈N,0<|m-n|≤1,若函数f(x)=mx+1-n的零点x∈(k,k+1)k∈Z,则k= .