题目内容
16.已知变量x,y满足约束条件$\left\{\begin{array}{l}{x+2y-3≤0}\\{x+3y-3≥0}\\{y-1≤0}\end{array}\right.$,则F(x,y)=log2(y+1)+log${\;}_{\frac{1}{2}}$(x+1)的最小值为-2.分析 由约束条件作出可行域,结合 的几何意义求出可行域内的动点与定点(-2,0)连线的斜率的最值得答案.
解答 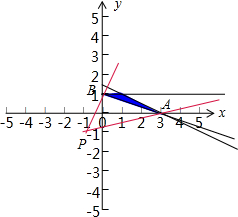 解:F(x,y)=log2(y+1)+log${\;}_{\frac{1}{2}}$(x+1)
解:F(x,y)=log2(y+1)+log${\;}_{\frac{1}{2}}$(x+1)
可得F(x,y)=log2$\frac{y+1}{x+1}$,x>-1,y>-1,
由约束条件$\left\{\begin{array}{l}{x+2y-3≤0}\\{x+3y-3≥0}\\{y-1≤0}\end{array}\right.$作出可行域如图,
$\frac{y+1}{x+1}$的几何意义为可行域内的动点与定点(-1,-1)连线的斜率,
kPA=$\frac{0+1}{3+1}$=$\frac{1}{4}$,kPB=$\frac{1+1}{0+1}$=2.∵得y=log2x是增函数,
∴F(x,y)=log2$\frac{y+1}{x+1}$,
则F(x,y)=log2(y+1)+log${\;}_{\frac{1}{2}}$(x+1)=log2$\frac{y+1}{x+1}$的最小值为:F(3,0)=log2$\frac{1}{4}$=-2.
故答案为:-2.
点评 本题考查了简单的线性规划,考查了数形结合的解题思想方法和数学转化思想方法,注意对数的运算法则,是中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
6.已知sin(π+α)=$\frac{\sqrt{3}}{2}$,则cos(α-$\frac{π}{2}$)的值是( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
11.“p∧q为假命题”是“¬p为真命题”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
5.复数$\frac{i}{2+i}$(i是虚数单位)的模长是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | $\frac{\sqrt{5}}{3}$ | D. | $\frac{\sqrt{5}}{5}$ |
11.$-\frac{29π}{6}$是( )
| A. | 第一象限的角 | B. | 第二象限的角 | C. | 第三象限的角 | D. | 第四象限的角 |