题目内容
（本题满分12分） 设椭圆 C1：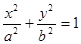
（
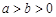）的一个顶点与抛物线 C2：
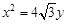的焦点重合，F1，F2 分别是椭圆的左、右焦点，离心率 
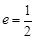，过椭圆右焦点 F2 的直线 
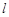与椭圆 C 交于 M，N 两点．
（I）求椭圆C的方程；
（II）是否存在直线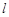，使得 
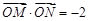，若存在，求出直线 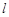的方程；若不存在，说明理由；
（III）若 AB 是椭圆 C 经过原点 O 的弦，MN//AB，求证：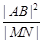
为定值．
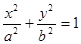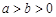（）的一个顶点与抛物线 C2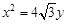： 的焦点重合，F1，F2 分别是椭圆的左、右焦点，离心率 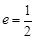，过椭圆右焦点 F2 的直线 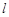与椭圆 C 交于 M，N 两点．（I）求椭圆C的方程；
（II）是否存在直线
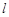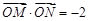，使得 ，若存在，求出直线 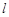的方程；若不存在，说明理由；（III）若 AB 是椭圆 C 经过原点 O 的弦，MN//AB，求证：
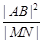为定值．解（1）椭圆的标准方程为
（2）直线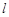的方程为
或
（3）定值
（2）直线
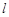的方程为或 （3）定值
略
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
，点
在
所在的平面内运动且保持
，则
的最大值和最小值分别是( )
和
.
是椭圆
的左、右焦点，点
在椭圆上运动，则
的最大值是_____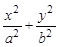
=1（a＞b＞0）的一个顶点和一个焦点，则此椭圆的离心率e=
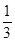
,动圆M过点F且与直线
相切。
交曲线L于A、B两点，求｜AB｜的值。
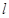相交所得的弦恰好被P平分，则此椭圆的离心率是 ；
、
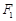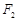是椭圆C：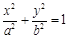
（
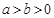）的两个焦点，P为椭圆C上的一点，且
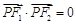。若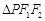
的面积为9，则
_________。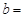