题目内容
【题目】设△ABC 的内角 A,B,C 的对边分别是a,b,c,且 ![]() a=
a= ![]() b cosC+c sinB. (Ⅰ)求角B 的大小;
b cosC+c sinB. (Ⅰ)求角B 的大小;
(Ⅱ)若点M 为BC的中点,且 AM=AC,求sin∠BAC.
【答案】解:(Ⅰ)∵ ![]() 由正弦定理
由正弦定理 ![]()
有 ![]()
又A=π﹣(B+C)即 ![]()
∴ ![]()
∴ ![]() ∴
∴ ![]()
因为0<B<π∴ ![]()
(Ⅱ)解法一:设∠BAC=θ,则 ![]() △ABC中,
△ABC中, 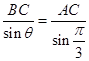
△ABM中, 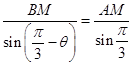
∵AM=AC,BC=2BM∴ 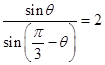
∴ ![]()
由平方关系得 ![]()
解法二:取CM中点D,连接AD,则AD⊥CM,
设CD=x,则BD=3x,
由(Ⅰ)知 ![]() ,∴
,∴ ![]()
由 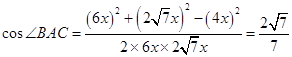
由平方关系得 ![]()
【解析】(Ⅰ) ![]() ,由正弦定理
,由正弦定理 ![]() ,代入化简利用和差公式即可得出.(Ⅱ)解法一:设∠BAC=θ,则
,代入化简利用和差公式即可得出.(Ⅱ)解法一:设∠BAC=θ,则 ![]() ,在△ABC中与△ABM中,利用正弦定理化简即可得出.解法二:取CM中点D,连接AD,则AD⊥CM,设CD=x,则BD=3x,由(Ⅰ)知
,在△ABC中与△ABM中,利用正弦定理化简即可得出.解法二:取CM中点D,连接AD,则AD⊥CM,设CD=x,则BD=3x,由(Ⅰ)知 ![]() ,可得
,可得 ![]() ,利用余弦定理与正弦定理即可得出.
,利用余弦定理与正弦定理即可得出.
【考点精析】通过灵活运用正弦定理的定义,掌握正弦定理:![]() 即可以解答此题.
即可以解答此题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
