题目内容
【题目】已知点P（ 
，1）和椭圆C： 
+ 
=1．
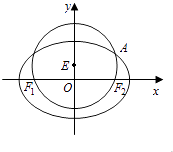
（1）设椭圆的两个焦点分别为F1 ， F2 ， 试求△PF1F2的周长及椭圆的离心率；
（2）若直线l： x﹣2y+m=0（m≠0）与椭圆C交于两个不同的点A，B，设直线PA与PB的斜率分别为k1 ， k2 ， 求证：k1+k2=0．
【答案】
（1）解：椭圆C： 
+ 
=1的a=2，b= 
，c= 
= ，
点P（ ，1）在椭圆C上，由椭圆定义可得|PF1|+|PF2|=2a=4，
△PF1F2的周长为2a+2c=4+2 ；
椭圆的离心率为e= 
= 
；
（2）证明：联立直线 x﹣2y+m=0和椭圆x2+2y2=4，
可得4x2+2 mx+m2﹣8=0，
由直线与椭圆有两个交点，且直线不过点P，
可得△=8m2﹣4×4（m2﹣8）＞0，且m≠0，
解得﹣4＜m＜0或0＜m＜4．
设A（x1，y1），B（x2，y2），
则x1+x2=﹣ m，x1x2= 
，
y1= 
，y2= 
，
则k1+k2= 
+ 
= 
+ 
= + 
+ 
= + 
= + 
= ﹣ 
=0．
【解析】（1）求得椭圆的a，b，c，可得P在椭圆上，运用椭圆的定义，即可得到△PF1F2的周长和椭圆的离心率；（2）联立直线和椭圆方程，可得x的二次方程，运用判别式大于0，以及韦达定理，结合直线的斜率公式，化简整理，即可得证．
练习册系列答案
课时训练江苏人民出版社系列答案
相关题目
