题目内容
在数学中“所有”一词,叫做全称量词,用符号“?”表示;“存在”一词,叫做存在量词,用符号“?”表示.
设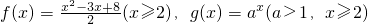 .
.
①?x0∈[2,+∞),使f(x0)=m成立,则实数m的取值范围为________;
②若?x1∈[2,+∞),?x2∈[2,+∞)使得f(x1)=g(x2),则实数a的取值范围为________.
[3,+∞) 
分析:①先对函数配方,求出其对称轴,判断出其在给定区间上的单调性进而求出函数值的范围,即可求出实数m的取值范围;
②先利用单调性分别求出两个函数的值域,再比较即可求出实数a的取值范围.
解答:①f(x)= (x-
(x- )2+
)2+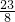 ,
,
∴函数在[2,+∞)上为增函数,∴f(x)≥f(2)=3,
即实数m的取值范围是[3,+∞);
②由①知,函数f(x)的值域是[3,+∞),又g(x)的值域是[a2,+∞)
∵?x1∈[2,+∞),?x2∈[2,+∞)使得f(x1)=g(x2),
∴a2≤3
∵a>1,
∴1<a≤ .
.
故答案为:①[3,+∞)② .
.
点评:本题主要考查函数恒成立问题以及借助于单调性研究函数的值域,是对基础知识的综合考查,属于中档题目.

分析:①先对函数配方,求出其对称轴,判断出其在给定区间上的单调性进而求出函数值的范围,即可求出实数m的取值范围;
②先利用单调性分别求出两个函数的值域,再比较即可求出实数a的取值范围.
解答:①f(x)=
 (x-
(x- )2+
)2+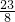 ,
,∴函数在[2,+∞)上为增函数,∴f(x)≥f(2)=3,
即实数m的取值范围是[3,+∞);
②由①知,函数f(x)的值域是[3,+∞),又g(x)的值域是[a2,+∞)
∵?x1∈[2,+∞),?x2∈[2,+∞)使得f(x1)=g(x2),
∴a2≤3
∵a>1,
∴1<a≤
 .
.故答案为:①[3,+∞)②
 .
.点评:本题主要考查函数恒成立问题以及借助于单调性研究函数的值域,是对基础知识的综合考查,属于中档题目.

练习册系列答案
相关题目
 ”表示;“存在”一词,叫做存在量词,用符号“
”表示;“存在”一词,叫做存在量词,用符号“ ”表示。设
”表示。设 ①若
①若 成立,则实数m取值范围为_____________;②若
成立,则实数m取值范围为_____________;②若 则实数a的取值范围为________。
则实数a的取值范围为________。