题目内容
2.函数y=sinx的图象沿x轴向左平移$\frac{π}{6}$个单位而得到的函数解析式可以是( )| A. | y=sin(x+$\frac{π}{6}$) | B. | y=sin(x-$\frac{π}{6}$) | C. | y=sinx+$\frac{π}{6}$ | D. | y=sinx-$\frac{π}{6}$ |
分析 由条件利用函数y=Asin(ωx+φ)的图象变换规律,得出结论.
解答 解:函数y=sinx的图象沿x轴向左平移$\frac{π}{6}$个单位而得到的函数解析式可以是y=sin(x+$\frac{π}{6}$),
故选:A.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
13.中心在原点,实轴长为4$\sqrt{3}$,离心率为e=$\sqrt{3}$,焦点在y轴上的双曲线的标准方程是( )
| A. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{36}$=1 | B. | $\frac{{y}^{2}}{12}$-$\frac{{y}^{2}}{36}$=1 | C. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{24}$=1 | D. | $\frac{{y}^{2}}{12}$-$\frac{{x}^{2}}{24}$=1 |
14.若∠A=22°,∠B=23°,则(1+tanA)(1+tanB)的值是( )
| A. | $\sqrt{3}$ | B. | 2 | C. | 1+$\sqrt{2}$ | D. | 2(tanA+tanB) |
11.已知数列{an}为等差数列,且a2=4,a6=12,则公差d=( )
| A. | 6 | B. | 3 | C. | 8 | D. | 2 |
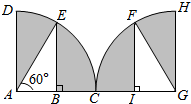 如图所示,两个四分之一圆面ACD和GCH交于点C点,AD=CH=10厘米,∠EAB=∠FGC=60°,EB与FI分别垂直于AC和GC,则阴影部分为85.28平方厘米.(π取3.14)
如图所示,两个四分之一圆面ACD和GCH交于点C点,AD=CH=10厘米,∠EAB=∠FGC=60°,EB与FI分别垂直于AC和GC,则阴影部分为85.28平方厘米.(π取3.14)