题目内容
6.为了解1200名学生对学校某项教改试验的意见,打算从中抽取一个容量为30的样本,考虑采用系统抽样,则分段间隔为40.分析 根据系统抽样的步骤,得到分段的间隔.
解答 解:由题意知本题是一个系统抽样,
总体中个体数是1200,样本容量是30,
根据系统抽样的步骤,得到分段的间隔K=$\frac{1200}{30}$=40,
故答案为:40.
点评 系统抽样时将整个的编号分段要确定分段的间隔,当总体个数除以样本容量是整数时,则间隔确定,当不是整数时,通过从总体中删除一些个体(用简单随机抽样的方法)使剩下的总体中个体的个数能被样本容量整除.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
16.设函数f(x)在R上存在导数f′(x),?x∈R,有f(-x)+f(x)=2x2,在(0,+∞)上f′(x)>2x,若f(2-m)+4m-4≥f(m),则实数m的取值范围为( )
| A. | -1≤m≤1 | B. | m≤1 | C. | -2≤m≤2 | D. | m≥2 |
14.已知双曲线的中心为原点,离心率e=$\sqrt{5}$,且它的一个焦点与抛物线x2=-8$\sqrt{5}$y的焦点重合,则此双曲线方程为( )
| A. | $\frac{y^2}{16}-\frac{x^2}{4}=1$ | B. | $\frac{y^2}{4}-\frac{x^2}{16}=1$ | C. | $\frac{x^2}{16}-\frac{y^2}{4}=1$ | D. | $\frac{x^2}{4}-\frac{y^2}{16}=1$ |
18.在△ABC中,根据下列条件解三角形,则其中有两个解的是( )
| A. | a=80,b=61,A=60° | B. | a=10,b=14,A=30° | ||
| C. | b=23,A=45°,B=30° | D. | a=61,c=47,A=120° |
15.已知f(x)为R上的可导函数,且对x∈R,均有f(x)>f′(x),则有( )
| A. | e2016f(-2016)<f(0),f(2016)<e2016f(0) | B. | e2016f(-2016)>f(0),f(2016)>e2016f(0) | ||
| C. | e2016f(-2016)<f(0),f(2016)>e2016f(0) | D. | e2016f(-2016)>f(0),f(2016)<e2016f(0) |
16.设变量x,y满足约束条件$\left\{\begin{array}{l}x+y-2≥0\\ x-y-2≤0\\ y≥1\end{array}\right.$,则目标函数z=x+2y( )
| A. | 有最小值3,无最大值 | B. | 有最小值5,无最大值 | ||
| C. | 有最大值3,无最小值 | D. | 有最大值5,无最小值 |
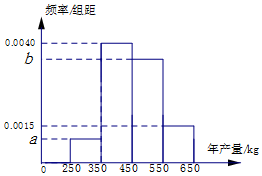 某人种植一种经济作物,根据以往的年产量数据,得到年产量频率分布直方图如图所示,以各区间中点值作为该区间的年产量,得到平均年产量为455kg,已知当年产量低于350kg时,单位售价为20元/kg,若当年产量不低于350kg而低于550时,单位售价为15元/kg,当年产量不低于550kg时,单位售价为10元/kg.
某人种植一种经济作物,根据以往的年产量数据,得到年产量频率分布直方图如图所示,以各区间中点值作为该区间的年产量,得到平均年产量为455kg,已知当年产量低于350kg时,单位售价为20元/kg,若当年产量不低于350kg而低于550时,单位售价为15元/kg,当年产量不低于550kg时,单位售价为10元/kg.