题目内容
已知函数f(x)=x-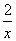 ,g(x)=a(2-ln x)(a>0).若曲线y=f(x)与曲线y=g(x)在x=1处的切线斜率相同,求a的值,并判断两条切线是否为同一条直线.
,g(x)=a(2-ln x)(a>0).若曲线y=f(x)与曲线y=g(x)在x=1处的切线斜率相同,求a的值,并判断两条切线是否为同一条直线.
解:根据题意有
曲线y=f(x)在x=1处的切线斜率为
f′(1)=3,
曲线y=g(x)在x=1处的切线斜率为
g′(1)=-a.
所以f′(1)=g′(1),即a=-3.
曲线y=f(x)在x=1处的切线方程为y-f(1)=3(x-1),又f(1)=-1,
得:y+1=3(x-1),即切线方程为3x-y-4=0.
曲线y=g(x)在x=1处的切线方程为y-g(1)=3(x-1).又g(1)=-6.
得y+6=3(x-1),即切线方程为3x-y-9=0,所以,两条切线不是同一条直线.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 的图像与函数y=kx-2的图像恰有两个交点,则实数k的取值范围是________.
的图像与函数y=kx-2的图像恰有两个交点,则实数k的取值范围是________.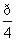 的旋转性的是( )
的旋转性的是( )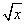 B.y=ln x C.y=
B.y=ln x C.y=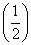 x D.y=x2
x D.y=x2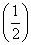 ,c=f(3),则( )
,c=f(3),则( )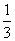 x3-
x3- x2-40x(x>0),为使耗电量最小,则速度应定为________.
x2-40x(x>0),为使耗电量最小,则速度应定为________.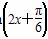 +2a+b,当x∈
+2a+b,当x∈ 时,-5≤f(x)≤1.
时,-5≤f(x)≤1. 且lg g(x)>0,求g(x)的单调区间.
且lg g(x)>0,求g(x)的单调区间.