题目内容
已知椭圆
=1,过点P（2，1）引一条弦，使它在这点被平分，求此弦所在的直线方程.
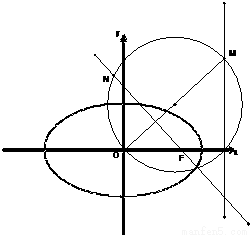
解法一：如图，设弦与椭圆的两交点坐标为A（x1,y1）、B(x2,y2).又P(2,1),
∴
①-②得（x1-x2)(x1+x2)+4(y1-y2)(y1+y2)=0,
∴
=kAB.
∴lAB的方程为y-1=-
(x-2).
解法二：依题意知，过点P的直线的斜率是存在的.
设过点P(2,1)的直线方程为y-1=k(x-2).
联立方程组
消去y,得
(4k2+1)x2-8k(2k-1)x+4k2-16k-12=0.
设弦与椭圆的两交点为A(x1,y1)、B(x2,y2),又中点P(2,1)，由韦达定理，得
=2,解得k=-
.
因为点P(2,1)在椭圆
=1内，所以直线AB必与椭圆相交.
直线AB的方程为y-1=-
(x-2),即x+2y-4=0为所求.
练习册系列答案
相关题目
+
=1,过点P(2，1)引一条弦，使它在这点被平分，求此弦所在的直线方程.
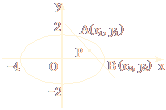
，过点P（1，1）作直线l与椭圆交于M、N两点．
+
=1经过点P（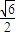
，
），离心率是
，动点M（2，t）（t＞0）