题目内容
已知椭圆C过点P(1,| 3 | 2 |
(1)求椭圆C的方程;
(2)过点F1的直线交椭圆于A、B两点,求线段AB的中点的轨迹方程.
分析:(1)设出椭圆的方程,将P的坐标代入椭圆的方程得到关于a,b的等式,再根据椭圆的三个参数的关系列出关于a,b,c的另一个等式,解方程组求出a,b的值即得到椭圆的方程.
(2)设出直线AB的方程,将直线的方程与椭圆方程联立,消去x得到关于y的二次方程,利用韦达定理表示出中点的坐标,消去参数m得到中点的轨迹方程.
(2)设出直线AB的方程,将直线的方程与椭圆方程联立,消去x得到关于y的二次方程,利用韦达定理表示出中点的坐标,消去参数m得到中点的轨迹方程.
解答:解:(1)由题意可知,c=1,a2=b2+1
设椭圆的方程为
+
=1(a>b>0)…即
+
=1
因为点P在椭圆上,所以
+
=1,解得b2=3,
所以椭圆方程为
+
=1
(2)解:设过点F1的直线方程为:x=my-1
代入
+
=1,得:
+
=1
整理得(3m2+4)y2-6my-9=0y1+y2=
同理可得:x1+x2=
设线段AB的中点为M(x,y),则
整理得:3x2+4y2+3x=0
当y=0时,易知线段AB的中点为原点,满足上述方程.
综上所述,所求的方程为:3x2+4y2+3x=0
设椭圆的方程为
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| 1+b2 |
| y2 |
| b2 |
因为点P在椭圆上,所以
| 1 |
| 1+b2 |
| 9 |
| 4b2 |
所以椭圆方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)解:设过点F1的直线方程为:x=my-1
代入
| x2 |
| 4 |
| y2 |
| 3 |
| (my-1)2 |
| 4 |
| y2 |
| 3 |
整理得(3m2+4)y2-6my-9=0y1+y2=
| 6m |
| 3m2+4 |
同理可得:x1+x2=
| -8 |
| 3m2+4 |
设线段AB的中点为M(x,y),则
|
整理得:3x2+4y2+3x=0
当y=0时,易知线段AB的中点为原点,满足上述方程.
综上所述,所求的方程为:3x2+4y2+3x=0
点评:求圆锥曲线的方程问题,一般利用待定系数法,注意椭圆中的三个参数的关系与双曲线中的三个参数关系的区别;解决直线与圆锥曲线的位置关系问题,一般将直线的方程与圆锥曲线的方程联立,利用韦达定理找突破口.

练习册系列答案
相关题目
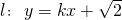 ,过点P(1,1)作直线l与椭圆交于M、N两点.
,过点P(1,1)作直线l与椭圆交于M、N两点. ,过点P(1,1)作直线l与椭圆交于M、N两点.
,过点P(1,1)作直线l与椭圆交于M、N两点. ),两个焦点分别为F1(-1,0),F2(1,0).
),两个焦点分别为F1(-1,0),F2(1,0).