题目内容
已知椭圆 ,过点P(1,1)作直线l与椭圆交于M、N两点.
,过点P(1,1)作直线l与椭圆交于M、N两点.(1)若点P平分线段MN,试求直线l的方程;
(5)设与满足(1)中条件的直线l平行的直线与椭圆交于A、B两点,AP与椭圆交于点C,BP与椭圆交于点D,求证:CD∥AB.
【答案】分析:(1)设M(xM,yM),N(xN,yN),则有xM+xN=2,yM+yN=2,利用点差法,可得 ,从而可求直线l的方程;
,从而可求直线l的方程;
(2)设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),且 ,
, ,可得
,可得 ,
, ,将点A、C的坐标分别代入椭圆方程,化简可得
,将点A、C的坐标分别代入椭圆方程,化简可得 ,同理有
,同理有 ,由此可得λ1=λ2,故可证得结论.
,由此可得λ1=λ2,故可证得结论.
解答:(1)解:设M(xM,yM),N(xN,yN),则有xM+xN=2,yM+yN=2. ①
① ②
②
①-②化简可得 +
+ =0
=0
∴ .
.
故直线l的方程为 ,即x+2y-3=0.(5分)
,即x+2y-3=0.(5分)
(2)证明:设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),且 ,
,
∴1-x1=λ1(x3-1),1-y1=λ1(y3-1)
∴ ,
,
将点A、C的坐标分别代入椭圆方程: ①,
①, ②
②
②× -①,并约去1+λ1得
-①,并约去1+λ1得 ③
③
同理有 ④
④
④-③可得 +
+ =λ2-λ1
=λ2-λ1
∵ ,∴
,∴ +
+ =0
=0
∴
即 ,即λ1=λ2,
,即λ1=λ2,
所以CD∥AB.(12分)
点评:本题考查直线与椭圆的位置关系,考查点差法的运用,解题的关键是设点,利用点差法解题.
 ,从而可求直线l的方程;
,从而可求直线l的方程;(2)设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),且
 ,
, ,可得
,可得 ,
, ,将点A、C的坐标分别代入椭圆方程,化简可得
,将点A、C的坐标分别代入椭圆方程,化简可得 ,同理有
,同理有 ,由此可得λ1=λ2,故可证得结论.
,由此可得λ1=λ2,故可证得结论.解答:(1)解:设M(xM,yM),N(xN,yN),则有xM+xN=2,yM+yN=2.
 ①
① ②
②①-②化简可得
 +
+ =0
=0∴
 .
.故直线l的方程为
 ,即x+2y-3=0.(5分)
,即x+2y-3=0.(5分)(2)证明:设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),且
 ,
,
∴1-x1=λ1(x3-1),1-y1=λ1(y3-1)
∴
 ,
,
将点A、C的坐标分别代入椭圆方程:
 ①,
①, ②
②②×
 -①,并约去1+λ1得
-①,并约去1+λ1得 ③
③同理有
 ④
④④-③可得
 +
+ =λ2-λ1
=λ2-λ1∵
 ,∴
,∴ +
+ =0
=0∴

即
 ,即λ1=λ2,
,即λ1=λ2,所以CD∥AB.(12分)
点评:本题考查直线与椭圆的位置关系,考查点差法的运用,解题的关键是设点,利用点差法解题.

练习册系列答案
相关题目
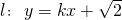 ,过点P(1,1)作直线l与椭圆交于M、N两点.
,过点P(1,1)作直线l与椭圆交于M、N两点. ,过点P(1,1)作直线l与椭圆交于M、N两点.
,过点P(1,1)作直线l与椭圆交于M、N两点. ,过点P(1,1)作直线l与椭圆交于M、N两点.
,过点P(1,1)作直线l与椭圆交于M、N两点. ),两个焦点分别为F1(-1,0),F2(1,0).
),两个焦点分别为F1(-1,0),F2(1,0).