题目内容
若双曲线
-y2=1过点P（2
，1），则双曲线的焦点坐标是
- A.（
，0） - B.（
，0） - C.（0，）
- D.（0，）
B
分析：先将点P代入双曲线，求得a2=4，∴c2=5，从而可求双曲线的焦点坐标．
解答：将点P（2，1）代入双曲线-y2=1，解得a2=4，
∴c2=5，∴双曲线的焦点坐标是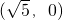
，
故选B．
点评：本题主要考查曲线与方程的关系，考查双曲线的几何性质，难度不大
分析：先将点P代入双曲线，求得a2=4，∴c2=5，从而可求双曲线的焦点坐标．
解答：将点P（2
，1）代入双曲线-y2=1，解得a2=4，∴c2=5，∴双曲线的焦点坐标是
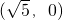，故选B．
点评：本题主要考查曲线与方程的关系，考查双曲线的几何性质，难度不大
练习册系列答案
快乐5加2金卷系列答案
相关题目
若双曲线mx2-y2=1过抛物线y2=2x的焦点，则双曲线的离心率等于（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
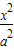-y2=1过点P（2
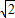，1），则双曲线的焦点坐标是（ ）
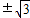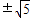，0）
，0）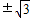
）
）
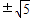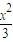-y2=1的一个焦点F作与x轴不垂直的直线交双曲线于A、B两点，线段AB的垂直平分线交X轴于点M则
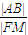为定值，且定值为
．
+
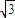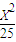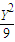=1的类似的正确命题，并加以证明；