题目内容
命题“若过双曲线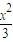 -y2=1的一个焦点F作与x轴不垂直的直线交双曲线于A、B两点,线段AB的垂直平分线交X轴于点M则
-y2=1的一个焦点F作与x轴不垂直的直线交双曲线于A、B两点,线段AB的垂直平分线交X轴于点M则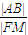 为定值,且定值为
为定值,且定值为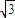 .
.(1)试类比上述命题,写出一个关于椭圆C:
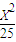 +
+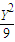 =1的类似的正确命题,并加以证明;
=1的类似的正确命题,并加以证明;(2)试推广(1)中的命题,给出关于圆锥曲线(椭圆、双曲线、抛物线)的统一的一般性命题(不证明).
【答案】分析:(1)关于椭圆C的类似命题是:过椭圆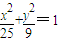 的一个焦点F2(4,0)作与x轴不垂直的直线交椭圆于A、B两点,线段AB的垂直平分线交x轴于点M,则
的一个焦点F2(4,0)作与x轴不垂直的直线交椭圆于A、B两点,线段AB的垂直平分线交x轴于点M,则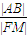 为定值,且定值为
为定值,且定值为 .
.
证明:设直线l为:y=k(x-4),当k=0时,l与x轴重合,|AB|=10,|FM|=4,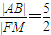 .当k≠0时,由
.当k≠0时,由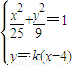 ,得(25k2+9)x2-8×25k2+25(16k2-9)=0,由根的判别式和韦达定理知AB的垂直平分线方程为:
,得(25k2+9)x2-8×25k2+25(16k2-9)=0,由根的判别式和韦达定理知AB的垂直平分线方程为: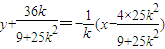 ,由此能够证明
,由此能够证明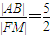 .
.
(2)过圆锥曲线E的一个焦点F作与x轴不垂直的直线交曲线E于A、B两点,线段AB的垂直平分线交x轴于点M,由此知则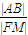 为定值
为定值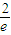 .
.
解答:解:(1)关于椭圆C的类似命题是:
过椭圆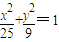 的一个焦点F2(4,0)作与x轴不垂直的直线交椭圆于A、B两点,线段AB的垂直平分线交x轴于点M,则
的一个焦点F2(4,0)作与x轴不垂直的直线交椭圆于A、B两点,线段AB的垂直平分线交x轴于点M,则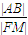 为定值,且定值为
为定值,且定值为 .
.
证明:由于l与x轴不垂直,设直线l为:y=k(x-4),
①当k=0时,l与x轴重合,|AB|=10,|FM|=4,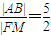 .
.
②当k≠0时,由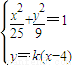 ,
,
消去y,得(25k2+9)x2-8×25k2+25(16k2-9)=0,
△=(8×25k2)2-4×25(25k2+9)(16k2-9)=4×25×92(k2+1),
设A(x1,y1),B(x2,y2),
AB中点N(x,y),
则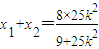 ,
,
∴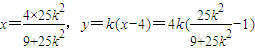 =
=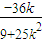 ,
,
AB的垂直平分线方程为: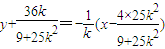 ,
,
令y=0,解得x= ,
,
∴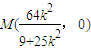 ,
,
∴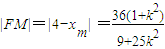 ,
,
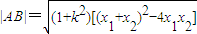
=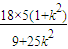 ,
,
∴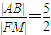 .
.
(2)过圆锥曲线E的一个焦点F作与x轴不垂直的直线交曲线E于A、B两点,
线段AB的垂直平分线交x轴于点M,则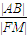 为定值,且定值为
为定值,且定值为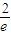 .
.
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.
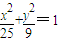 的一个焦点F2(4,0)作与x轴不垂直的直线交椭圆于A、B两点,线段AB的垂直平分线交x轴于点M,则
的一个焦点F2(4,0)作与x轴不垂直的直线交椭圆于A、B两点,线段AB的垂直平分线交x轴于点M,则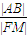 为定值,且定值为
为定值,且定值为 .
.证明:设直线l为:y=k(x-4),当k=0时,l与x轴重合,|AB|=10,|FM|=4,
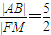 .当k≠0时,由
.当k≠0时,由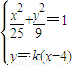 ,得(25k2+9)x2-8×25k2+25(16k2-9)=0,由根的判别式和韦达定理知AB的垂直平分线方程为:
,得(25k2+9)x2-8×25k2+25(16k2-9)=0,由根的判别式和韦达定理知AB的垂直平分线方程为: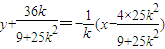 ,由此能够证明
,由此能够证明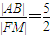 .
.(2)过圆锥曲线E的一个焦点F作与x轴不垂直的直线交曲线E于A、B两点,线段AB的垂直平分线交x轴于点M,由此知则
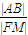 为定值
为定值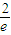 .
.解答:解:(1)关于椭圆C的类似命题是:
过椭圆
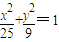 的一个焦点F2(4,0)作与x轴不垂直的直线交椭圆于A、B两点,线段AB的垂直平分线交x轴于点M,则
的一个焦点F2(4,0)作与x轴不垂直的直线交椭圆于A、B两点,线段AB的垂直平分线交x轴于点M,则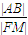 为定值,且定值为
为定值,且定值为 .
.证明:由于l与x轴不垂直,设直线l为:y=k(x-4),
①当k=0时,l与x轴重合,|AB|=10,|FM|=4,
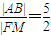 .
.②当k≠0时,由
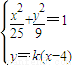 ,
,消去y,得(25k2+9)x2-8×25k2+25(16k2-9)=0,
△=(8×25k2)2-4×25(25k2+9)(16k2-9)=4×25×92(k2+1),
设A(x1,y1),B(x2,y2),
AB中点N(x,y),
则
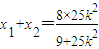 ,
,∴
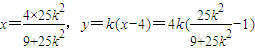 =
=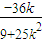 ,
,AB的垂直平分线方程为:
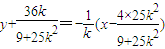 ,
,令y=0,解得x=
 ,
,∴
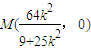 ,
,∴
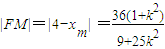 ,
,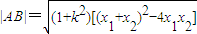
=
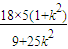 ,
,∴
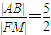 .
.(2)过圆锥曲线E的一个焦点F作与x轴不垂直的直线交曲线E于A、B两点,
线段AB的垂直平分线交x轴于点M,则
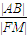 为定值,且定值为
为定值,且定值为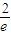 .
.点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
 =1两焦点F1,F2,则椭圆上存在六个不同点M,使得△F1MF2为直角三角形;
=1两焦点F1,F2,则椭圆上存在六个不同点M,使得△F1MF2为直角三角形; =1(a>0,b>0)的一个焦点作它的一条渐近线的垂线,垂足为M,O为坐标原点,则|OM|=a;
=1(a>0,b>0)的一个焦点作它的一条渐近线的垂线,垂足为M,O为坐标原点,则|OM|=a; 的两个焦点为F1,F2,则这个椭圆上存在六个不同的点M,使得△F1MF2为直角三角形;
的两个焦点为F1,F2,则这个椭圆上存在六个不同的点M,使得△F1MF2为直角三角形; 的一个焦点作它的一条渐近线的垂线,垂足为M,O为坐标原点,则|OM|=a;
的一个焦点作它的一条渐近线的垂线,垂足为M,O为坐标原点,则|OM|=a;