题目内容
(本小题满分14分)
已知数列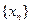 满足
满足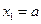 ,
,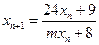
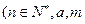 是实数).
是实数).
(1)若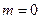 ,
,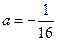 ,求通项
,求通项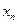 ;
;
(2)若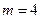 ,设数列
,设数列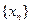 的前
的前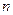 项和当
项和当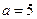 时为
时为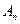 ,当
,当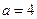 时为
时为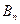 ,
,
求证: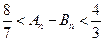
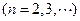 .
.
已知数列
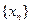 满足
满足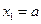 ,
,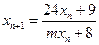
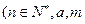 是实数).
是实数).(1)若
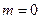 ,
,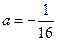 ,求通项
,求通项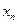 ;
;(2)若
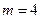 ,设数列
,设数列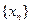 的前
的前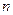 项和当
项和当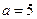 时为
时为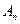 ,当
,当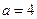 时为
时为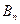 ,
,求证:
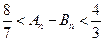
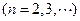 .
.(1) (2)见解析
(2)见解析
 (2)见解析
(2)见解析(1)解: 得
得 ,又
,又
∴ 是首项为
是首项为 ,公比为3的等比数列
,公比为3的等比数列
∴ ∴
∴
 …………4分
…………4分
(2)解法一:设 时,数列为
时,数列为 ,
, 时,数列为
时,数列为 ,又
,又
∴ ,由
,由 得
得 ,
,
 , ……
, …… ……6分
……6分
知 与
与 同号
同号
即与 同号,得
同号,得 ,由
,由
同理当 得
得 ,
, ∴
∴
∴
 …………9分
…………9分
∴ …………10分
…………10分
∴ …………12分
…………12分
又
 时
时 
综上
 ………14分
………14分
(2)解法二: ∴
∴
设 时,数列为
时,数列为 ,
, ,
, 7分
7分
设 时,数列为
时,数列为 同理
同理 ……9分
……9分
∴
令 则
则 (∵
(∵ )
)
∴
 ① ……11分
① ……11分
再证
即 ∵
∵ 得证
得证
∴ ②
②
由①、②知

 …………14分
…………14分
 得
得 ,又
,又
∴
 是首项为
是首项为 ,公比为3的等比数列
,公比为3的等比数列∴
 ∴
∴
 …………4分
…………4分(2)解法一:设
 时,数列为
时,数列为 ,
, 时,数列为
时,数列为 ,又
,又
∴
 ,由
,由 得
得 ,
,
 , ……
, …… ……6分
……6分知
 与
与 同号
同号即与
 同号,得
同号,得 ,由
,由
同理当
 得
得 ,
, ∴
∴
∴

 …………9分
…………9分∴
 …………10分
…………10分∴
 …………12分
…………12分又

 时
时 
综上

 ………14分
………14分(2)解法二:
 ∴
∴
设
 时,数列为
时,数列为 ,
, ,
, 7分
7分设
 时,数列为
时,数列为 同理
同理 ……9分
……9分∴

令
 则
则 (∵
(∵ )
)∴

 ① ……11分
① ……11分再证

即
 ∵
∵ 得证
得证∴
 ②
②由①、②知


 …………14分
…………14分
练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
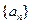 的前
的前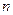 项和为
项和为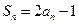 ,数列
,数列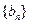 满足
满足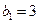 ,
,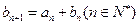 .
.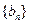 的通项公式; (2)求数列
的通项公式; (2)求数列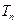 ;
;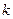 ,使得数列
,使得数列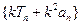 为等差数列,证明你的结论.
为等差数列,证明你的结论.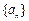 的首项为
的首项为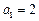 ,前
,前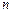 项和为
项和为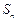 ,且对任意的
,且对任意的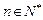 ,
,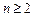 时,
时,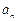 总是
总是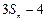 与
与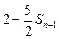 的等差中项.
的等差中项.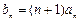 ,
,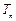 是数列
是数列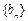 的前
的前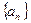 的公差
的公差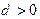 ,满足
,满足 ,
,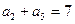 ,设
,设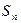 ,则
,则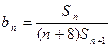 的最大值为
的最大值为 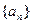 的前n项和为
的前n项和为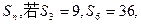 则
则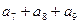 =" " ( )
=" " ( )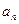 }的首项为
}的首项为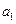 =
=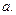 公比为q,则
公比为q,则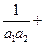
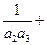 …
…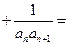 __________。
__________。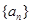 中,已知
中,已知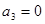 ,
,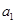 =4,则公差d等于 ( )
=4,则公差d等于 ( )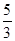 C.- 2 D 3
C.- 2 D 3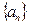 中,已知
中,已知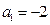 ,
,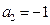 ,
,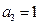 ,若对任意正整数
,若对任意正整数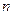 ,有
,有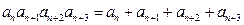 ,且
,且
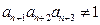 ,则该数列的前2010 项和
,则该数列的前2010 项和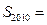 ( )
( )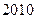 .
.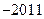 .
.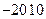 .
.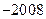 .
.