题目内容
已知向量 ,函数
,函数 .
.
(1)求函数 的对称中心;
的对称中心;
(2)在 中,
中, 分别是角
分别是角 对边,且
对边,且 ,且
,且 ,求
,求 的取值范围.
的取值范围.
 ,函数
,函数 .
.(1)求函数
 的对称中心;
的对称中心; (2)在
 中,
中, 分别是角
分别是角 对边,且
对边,且 ,且
,且 ,求
,求 的取值范围.
的取值范围.(1)  (2)
(2)
 (2)
(2)
试题分析:(1)此类问题往往是利用向量数量积定义及二倍角公式把f(x)化简成f(x)
 或者f(x)
或者f(x) 的形式,然后利用从而由y=sinx或者y=cosx的对称中心求出f(x)的对称中心.(2)求范围问题往往利用函数的思想,因此本题需要转化到关于边或者三角的函数问题,由题意可知将用正弦定理将边的关系转化为三角关系,利用三角函数的值域来确定
的形式,然后利用从而由y=sinx或者y=cosx的对称中心求出f(x)的对称中心.(2)求范围问题往往利用函数的思想,因此本题需要转化到关于边或者三角的函数问题,由题意可知将用正弦定理将边的关系转化为三角关系,利用三角函数的值域来确定 的范围.
的范围.(1)f(x)=

 令
令 ,得出
,得出 ,函数f(x)的对称中心
,函数f(x)的对称中心 .
.(2)f(C)=
 ,
, ,因为C为锐角,
,因为C为锐角, ,由正弦定理
,由正弦定理 a=2sinA,b=2sinB,
a=2sinA,b=2sinB,
 ,A>B>C=
,A>B>C= ,
, .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
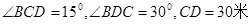 ,并在点C测得塔顶A的仰角为
,并在点C测得塔顶A的仰角为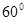 ,求塔高AB.
,求塔高AB.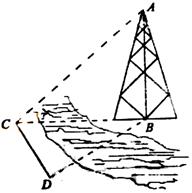
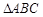 中,
中,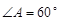 ,
,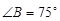 ,
,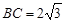 ,则
,则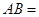 .
.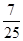
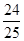
 、
、 、
、 分别是
分别是 的三个内角
的三个内角 、
、 、
、 所对的边
所对的边 求
求 ,试判断
,试判断 ,求角A;(2)若
,求角A;(2)若 ,求△ABC的面积.
,求△ABC的面积. 中,
中, ,点
,点 在
在 边上,且
边上,且 ,
, .
. ;
; ,
, 的长.
的长.
 分别为角A、B、C所对的边,且
分别为角A、B、C所对的边,且 .
. ,且
,且
 ,求
,求 的值.
的值. 中,内角
中,内角 的对边分别为
的对边分别为 ,若
,若 ,
, ,
, ,则
,则 等于( )
等于( )
