题目内容
设同时满足条件:①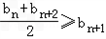 ;②bn∈M(n∈N+,M是与n无关的常数)的无穷数列{bn}叫“嘉文”数列.已知数列{an}的前n项和Sn满足:
;②bn∈M(n∈N+,M是与n无关的常数)的无穷数列{bn}叫“嘉文”数列.已知数列{an}的前n项和Sn满足: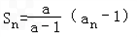 (a为常数,且
(a为常数,且
a≠0,a≠1).
(1)求{an}的通项公式;
(2)设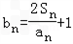 ,若数列{bn}为等比数列,求a的值,并证明此时
,若数列{bn}为等比数列,求a的值,并证明此时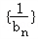 为“嘉文”数列.
为“嘉文”数列.
 ;②bn∈M(n∈N+,M是与n无关的常数)的无穷数列{bn}叫“嘉文”数列.已知数列{an}的前n项和Sn满足:
;②bn∈M(n∈N+,M是与n无关的常数)的无穷数列{bn}叫“嘉文”数列.已知数列{an}的前n项和Sn满足: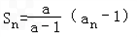 (a为常数,且
(a为常数,且a≠0,a≠1).
(1)求{an}的通项公式;
(2)设
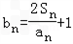 ,若数列{bn}为等比数列,求a的值,并证明此时
,若数列{bn}为等比数列,求a的值,并证明此时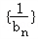 为“嘉文”数列.
为“嘉文”数列.解:(1)因为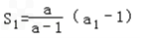 ,所以a1=a
,所以a1=a
当n≥2时,
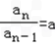 ,
,
即{an}以a为首项,a为公比的等比数列.
∴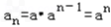 ;
;
(2)由(1)知,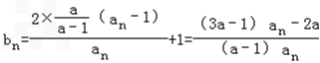 ,
,
若{bn}为等比数列,则有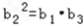 ,
,
而b1=3,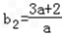 ,
,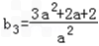 故
故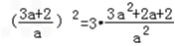 ,
,
解得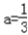 ,再将
,再将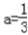 代入得:
代入得: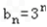 ,
,
其为等比数列,所以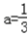 成立
成立
由于①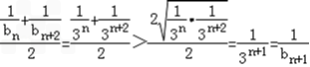
(或做差更简单:因为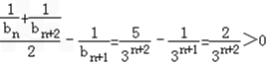 ,
,
所以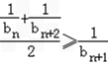 也成立)
也成立)
②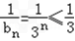 ,故存在
,故存在 ;
;
所以符合①②,故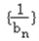 为“嘉文”数列
为“嘉文”数列
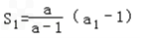 ,所以a1=a
,所以a1=a当n≥2时,

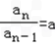 ,
,即{an}以a为首项,a为公比的等比数列.
∴
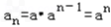 ;
; (2)由(1)知,
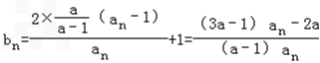 ,
,若{bn}为等比数列,则有
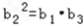 ,
,而b1=3,
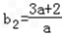 ,
,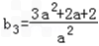 故
故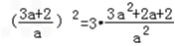 ,
,解得
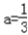 ,再将
,再将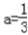 代入得:
代入得: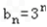 ,
,其为等比数列,所以
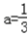 成立
成立由于①

(或做差更简单:因为
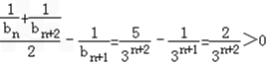 ,
,所以
 也成立)
也成立)②
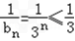 ,故存在
,故存在 ;
;所以符合①②,故
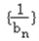 为“嘉文”数列
为“嘉文”数列
练习册系列答案
相关题目
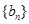 是首项为
是首项为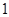 ,公比为
,公比为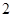 的等比数列.数列
的等比数列.数列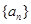 满足
满足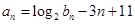 ,
,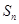 是
是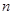 项和.
项和.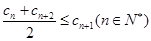 ;②
;② (
(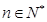 ,
,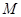 是与
是与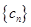 叫“特界”数列.判断(1)中的数列
叫“特界”数列.判断(1)中的数列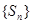 是否为“特界”数列,并说明理由.
是否为“特界”数列,并说明理由.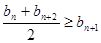 ;②
;②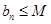 (
( ,
,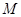 是与
是与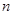 无关的常数)的无穷数列
无关的常数)的无穷数列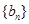 叫“嘉文”数列.已知数列
叫“嘉文”数列.已知数列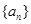 的前
的前 满足:
满足: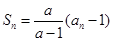 (
(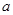 为常数,且
为常数,且 ,
,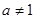 ).
).  ,若数列
,若数列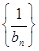 为“嘉文”数列.
为“嘉文”数列.