题目内容
(本小题满分12分)
设同时满足条件:①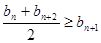 ;②
;②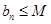 (
( ,
,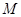 是与
是与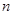 无关的常数)的无穷数列
无关的常数)的无穷数列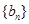 叫“嘉文”数列.已知数列
叫“嘉文”数列.已知数列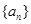 的前
的前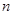 项和
项和 满足:
满足: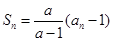 (
(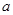 为常数,且
为常数,且 ,
,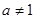 ).
).
(Ⅰ)求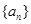 的通项公式;[来源:学*科*网Z*X*X*K]
的通项公式;[来源:学*科*网Z*X*X*K]
(Ⅱ)设 ,若数列
,若数列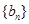 为等比数列,求
为等比数列,求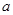 的值,并证明此时
的值,并证明此时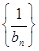 为“嘉文”数列.
为“嘉文”数列.
【答案】
解:(Ⅰ)因为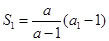 所以
所以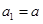
当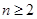 时,
时,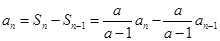
 ,即
,即 以
以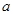 为首项,
为首项,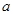 为公比的等比数列.
为公比的等比数列.
∴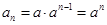 ;
……………………………………………4分
;
……………………………………………4分
(Ⅱ)由(Ⅰ)知,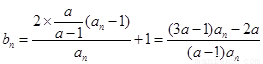 ,
,
若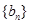 为等比数列,则有
为等比数列,则有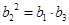 ,而
,而 ,
,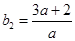 ,
,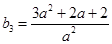
故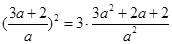 ,解得
,解得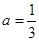 ………………………………7分
………………………………7分
再将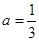 代入得:
代入得: ,其为等比数列,
所以
,其为等比数列,
所以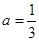 成立…………8分
成立…………8分
由于①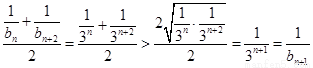 …………………10分
…………………10分
(或做差更简单:因为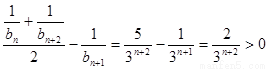 ,所以
,所以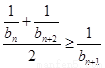 也成立)
也成立)
②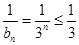 ,故存在
,故存在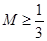 ;
;
所以符合①②,故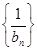 为“嘉文”数列………………………………………12分
为“嘉文”数列………………………………………12分
【解析】略

练习册系列答案
相关题目