Question

某班40人随机平均分成两组,两组学生一次考试的成绩情况如下表：

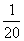
求全班的平均成绩和标准差.

 

Answer 1

解析：设第一组20名学生的成绩为

x_i(i=1,2,…,20),

    第二组20名学生的成绩为y_i(i=1,2,…,20),

    依题意有：90=(x₁+x₂+…+x₂₀),

80=(y₁+y₂+…+y₂₀),故全班平均成绩为：

(x₁+x₂+…+x₂₀+y₁+y₂+…+y₂₀)=(90×20+80×20)=85;

    又设第一组学生成绩的标准差为s₁,第二组学生成绩的标准差为s₂,则=(+…+-

20),

s₂²=(y₁²+y₂²+…+-20)(此处,=90,=80).

    又设全班40名学生的标准差为s,平均成绩为(=85),

    故有s²=(+…+++…+-40)

=(20+20+20+20-40)=(6²+4²+90²+80²-2×85²)=51.

s=