Question

设数列{a_n}的首项a₁=1，前n项和S_n满足关系式：3tS_n﹣（2t+3）S_n﹣1=3t（t＞0，n=2，3，4，…）

（1）求证：数列{a_n}是等比数列；

（2）设数列{a_n}是公比为f（t），作数列{b_n}，使（n=2，3，4，…），求和：b₁b₂﹣b₂b₃+b₃b₄﹣…+b_2n﹣1b_2n﹣b_2nb_2n+1；

（3）若t=﹣3，设c_n=log₃a₂+log₃a₃+log₃a₄+…+log₃a_n+1，T_n=++…+，求使k≥（7﹣2n）T_n（n∈N⁺）恒成立的实数k的范围．

Answer 1

考点：

等比关系的确定；数列的求和；数列与不等式的综合．

专题：

证明题；综合题；等差数列与等比数列．

分析：

（1）由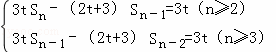可求得=（n=3，4，…），又a₁=1，a₂=，可证数列{a_n}是首项为1，公比为的等比数列；

（2）依题意可求得f（t）=+，b_n=f（）=，可知数列{b_2n﹣1}与{b_2n}是首项分别为1和，公差均为的等差数列，且b_2n=，从而可求得b₁b₂﹣b₂b₃+b₃b₄﹣…+b_2n﹣1b_2n﹣b_2nb_2n+1；

（3）可求得c_n=﹣，=﹣，数列{}的前n项和为﹣，对k≥（7﹣2n）T_n（n∈N⁺）化简得k≥对任意n∈N^*恒成立，再构造函数d_n=，对n分类讨论，研究函数，{d_n}与{c_n}的单调性即可求得k的取值范围．

解答：

解：（1）由S₁=a₁=1，S₂=a₁+a₂=1+a₂，得3t（1+a₂）﹣（2t+3）=3t，则a₂=，于是=，

又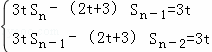两式相减得3ta_n﹣（2t+3）a_n﹣1=0，

于是=（n=3，4，…）

因此，数列{a_n}是首项为1，公比为的等比数列．

（2）按题意，f（t）==+，

故b_n=f（）=+b_n﹣1⇒b_n=1+（n﹣1）=，

由b_n=，可知数列{b_2n﹣1}与{b_2n}是首项分别为1和，公差均为的等差数列，且b_2n=，

于是b₁b₂﹣b₂b₃+b₃b₄﹣…+b_2n﹣1b_2n﹣b_2nb_2n+1

=b₂（b₁﹣b₃）+b₄（b₃﹣b₅）+…+b_2n（b_2n﹣1﹣b_2n+1）

=﹣（b₂+b₄+…+b_2n）

=﹣（2n²+3n）

（3）c_n=log₃a₁+log₃a₂+…+log₃a_n

=﹣（1+2+3+…+n）

=﹣．

故=﹣=﹣2（﹣）．

T_n=++…+

=﹣2[（1﹣）+（﹣）+…+（﹣）]

=﹣．

所以数列{}的前n项和为﹣．化简得k≥对任意n∈N^*恒成立．

设d_n=，则d_n+1﹣d_n=﹣=．

当n≥5，d_n+1≤d_n，{d_n}为单调递减数列，1≤n＜5，d_n+1＞d_n，{d_n}为单调递增数列．

当n≥5，c_n+1≤c_n，{c_n}为单调递减数列，当1≤n＜5，c_n+1＞c_n，{c_n}为单调递增数列．

=d₄＜d₅=，所以，n=5时，d_n取得最大值为．

所以，要使k≥对任意n∈N^*恒成立，k≥．

点评：

本题考查等比关系的确定，考查数列与不等式的综合，突出考查等差数列的求和与等比数列的证明，考查化归思想与分类讨论思想，属于难题．