题目内容
 如图,设计建造一个面积为4840m2的矩形蔬菜温室,其长与宽的比为λ(λ>1).沿温室的左、右两侧各留8m宽的空道,上、下两侧各留5m宽的空道.试确定温室的长和宽,使其占地(包括蔬菜温室及空道)面积最小.
如图,设计建造一个面积为4840m2的矩形蔬菜温室,其长与宽的比为λ(λ>1).沿温室的左、右两侧各留8m宽的空道,上、下两侧各留5m宽的空道.试确定温室的长和宽,使其占地(包括蔬菜温室及空道)面积最小.分析:设矩形温室宽为xm,则长为λxm,依题意有λx2=4840,记矩形温室的占地面积为S,则S=(λx+16)(x+10)=λx2+(10λ+16)x+160,代入利用基本不等式,即可求最值.
解答:解:设矩形温室宽为xm,则长为λxm,依题意有λx2=4840. …(2分)
记矩形温室的占地面积为S,则S=(λx+16)(x+10)=λx2+(10λ+16)x+160. …(5分)
将λ=
代入上式,整理得S=5000+16(x+
). …(8分)
根据均值定理,当x=
时,即x=55(此时λ=
>1)时,S取得最小值. …(11分)
此时,温室的长为λx=
×55=88 m. …(12分)
答:矩形温室的长为88m,宽为55m时,温室的占地面积最小. …(13分)
记矩形温室的占地面积为S,则S=(λx+16)(x+10)=λx2+(10λ+16)x+160. …(5分)
将λ=
| 4840 |
| x2 |
| 3025 |
| x |
根据均值定理,当x=
| 3025 |
| x |
| 8 |
| 5 |
此时,温室的长为λx=
| 8 |
| 5 |
答:矩形温室的长为88m,宽为55m时,温室的占地面积最小. …(13分)
点评:本题考查函数模型的建立,考查基本不等式的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
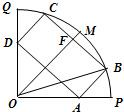 如图所示,某市政府决定在以政府大楼O为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径OM=R,∠MOP=45°,OB与OM之间的夹角为θ.
如图所示,某市政府决定在以政府大楼O为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径OM=R,∠MOP=45°,OB与OM之间的夹角为θ. 如图所示,某市政府决定在以政府大楼O为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径OM=R,∠MOP=45°,OB与OM之间的夹角为θ.
如图所示,某市政府决定在以政府大楼O为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径OM=R,∠MOP=45°,OB与OM之间的夹角为θ. 如图所示,某市政府决定在以政府大楼O为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径OM=R,∠MOP=45°,当点B位于何处时,图书馆的占地面积最大,最大面积是多少?
如图所示,某市政府决定在以政府大楼O为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径OM=R,∠MOP=45°,当点B位于何处时,图书馆的占地面积最大,最大面积是多少?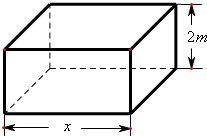 现要求建造一个容积为8m3,深为2m的长方体无盖水池(如图),如果池底和池壁的造价分别为120元/m2和80元/m2.
现要求建造一个容积为8m3,深为2m的长方体无盖水池(如图),如果池底和池壁的造价分别为120元/m2和80元/m2. 为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径
为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径 ,
, ,
,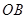 与
与 之间的夹角为
之间的夹角为 .
.
 的面积
的面积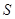 表示成
表示成