题目内容
一扇形的中心角为α，周长为8-π，若在直角坐标系中，当α角的始边与x角的正半轴重合时，x角的终边上的一点坐标为（3.5sin2，-3.5cos2），则扇形的面积为 ．
【答案】分析：先根据角的象限，利用其某种三角函数值求出其大小，再结合扇形弧长、面积公式解决．
解答：解：∵
＜2＜π，∴3.5sin2＞0，-3.5cos2＞0，P（3.5sin2，-3.5cos2）在第-象限，所以α是锐角，由任意角三角函数的定义及诱导公式得：sinα=
=-cos2=sin（2-
），
∵0＜2-
＜π，∴α=2-
．扇形的周长=2r+（2-
）r=8-π，∴r=2．扇形的面积为
αr 2=
×（2-
）×4=4-π．
故答案为：4-π．
点评：本题考查了三角函数诱导公式的应用，非特殊角大小求解，扇形弧长、面积公式．
解答：解：∵
＜2＜π，∴3.5sin2＞0，-3.5cos2＞0，P（3.5sin2，-3.5cos2）在第-象限，所以α是锐角，由任意角三角函数的定义及诱导公式得：sinα==-cos2=sin（2-），∵0＜2-
＜π，∴α=2-．扇形的周长=2r+（2-）r=8-π，∴r=2．扇形的面积为αr 2=×（2-）×4=4-π．故答案为：4-π．
点评：本题考查了三角函数诱导公式的应用，非特殊角大小求解，扇形弧长、面积公式．
练习册系列答案
相关题目
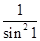D．