题目内容
18.对于定义域为R的函数f(x),若存在非零实数x0,使函数f(x)在(-∞,x0)和(x0,+∞)上与x轴均有交点,则称x0为函数f(x)的一个“界点”.则下列四个函数中,不存在“界点”的是( )| A. | f(x)=x2+bx-1(b∈R) | B. | f(x)=|x2-1| | C. | f(x)=2-|x-1| | D. | f(x)=x3+2x |
分析 判断函数与x轴交点个数,由此能求出结果.
解答 解:在A中,f(x)=x2+bx-1,b∈R,
△=b2+4>0,函数与x轴有两个不同的交点,故A存在“界点”;
在B中,f(x)=|x2-1|=$\left\{\begin{array}{l}{{x}^{2}-1,x≥1或x≤-1}\\{1-{x}^{2},-1<x<1}\end{array}\right.$,与x轴有两个交点(-1,0),(1,0),故B存在“界点”;
在C中,f(x)=2-|x-1|与x轴有两个交点(-1,0),(3,0),故C存在“界点”;
在D中,f(x)=x3+2x与x轴只有一个交点,故D不存在“界点”.
故选:D.
点评 本题考查函数是否存在“界点”的判断,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
8.关于x的方程($\frac{1}{3}$)|x|+a-1=0有解,则a的取值范围是( )
| A. | 0≤a<1 | B. | -1<a≤0 | C. | a≥1 | D. | a>0 |
9.已知m,n是两条不同的直线,α,β是两个不同的平面,则下列命题中正确的是( )
| A. | 若α⊥β,m∥α,则m⊥β | B. | 若m⊥α,n⊥β,且m⊥n,则α⊥β | ||
| C. | 若m?α,n?β,且α∥β,则m∥n | D. | 若m∥α,n∥β,且m∥n,则α∥β |
6.方程log5x-sin2x=0的根的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
3.直线2x-y-2=0绕它与y轴的交点逆时针旋转$\frac{π}{2}$所得的直线方程是( )
| A. | -x+2y-4=0 | B. | x+2y-4=0 | C. | -x+2y+4=0 | D. | x+2y+4=0 |
10.若a=60.3,b=log0.30.6,c=log6sin1,则a、b、c的大小关系为( )
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | b>c>a |
7.如图描述的是我国2014年四个季度与2015年前三个季度三大产业GDP累计同比贡献率,以下结论正确的是( )


| A. | 2015年前三个季度中国GDP累计比较2014年同期增速有上升的趋势 | |
| B. | 相对于2014年,2015年前三个季度第三产业对GDP的贡献率明显增加 | |
| C. | 相对于2014年,2015年前三个季度第二产业对GDP的贡献率明显增加 | |
| D. | 相对于2014年,2015年前三个季度第一产业对GDP的贡献率明显增加 |
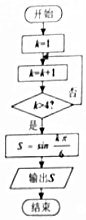
17.执行如图所示的程序框图,输出S的值为( )

| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |