题目内容
函数 的定义域为开区间(a,b),其导函数
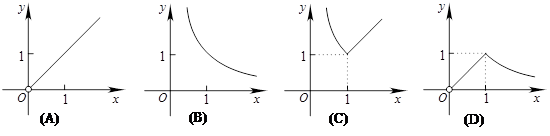
的定义域为开区间(a,b),其导函数 在(a,b)内的图像如下图所示,则函数
在(a,b)内的图像如下图所示,则函数 在开区间(a,b)内极小值点的个数有( )
在开区间(a,b)内极小值点的个数有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
A
解析试题分析:设 的图象与x轴交点分别为
的图象与x轴交点分别为 ,根据极小值点的概念可知只有
,根据极小值点的概念可知只有 为极小值点,故选A
为极小值点,故选A
考点:本题考查了极值的概念
点评:判断一个函数是否有极值,不能只求解 ,根据函数的极值定义,函数在某点处存在极值,则应在该点的左右邻域是单调的,并且单调性相反,因此,本题主要考查函数极值的概念
,根据函数的极值定义,函数在某点处存在极值,则应在该点的左右邻域是单调的,并且单调性相反,因此,本题主要考查函数极值的概念

练习册系列答案
相关题目
若方程 的根在区间
的根在区间 上,则
上,则 的值为( )
的值为( )
A. | B.1 |
C. 或2 或2 | D. 或1 或1 |
函数 的值域是( )
的值域是( )
A. | B. | C. | D. |
设偶函数 满足
满足
 ,则
,则 ( )
( )
A. | B. |
C. | D. |
已知 ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
已知函数 定义域是,则
定义域是,则 的定义域是( )
的定义域是( )
A. | B. | C.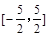 | D. |
函数 在下列区间内一定有零点的是 ( )
在下列区间内一定有零点的是 ( )
| A.[0,1] | B.[1,2] | C.[2,3] | D.[3,4] |
定义域为 的函数
的函数
 有四个单调区间,则实数
有四个单调区间,则实数 满足( )
满足( )
A. | B. | C. | D. |
 ,则函数
,则函数 的图象大致为( )
的图象大致为( )