题目内容
若方程 的根在区间
的根在区间 上,则
上,则 的值为( )
的值为( )
A. | B.1 |
C. 或2 或2 | D. 或1 或1 |
D
解析试题分析:在同一平面直角坐标系内,画出函数y=ln(x+1),y= 的图象,观察两图象的交点情况可知,交点位于区间(-1,0)或(1,2),所以k=
的图象,观察两图象的交点情况可知,交点位于区间(-1,0)或(1,2),所以k= 或1,选D。
或1,选D。
考点:本题主要考查函数的图象,函数方程思想。
点评:简单题,研究方程的根的情况,可转化成研究函数图象的交点情况。本题也可结合选项,代入验证。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数 ,则该函数是 ( )
,则该函数是 ( )
A.偶函数,且单调递增  | B.偶函数,且单调递减 |
| C.奇函数,且单调递增 | D.奇函数,且单调递减 |
函数y=log x+log2x2+2的值域是( )
x+log2x2+2的值域是( )
| A.(0,+∞) | B.[1,+∞) | C.(1,+∞) | D.R |
由表格中的数据可以判定方程 的一个零点所在的区间是
的一个零点所在的区间是 ,则
,则 的值为
的值为
 | -1 | 0 | 1 | 2 | 3 |
 | 0.37 | 1 | 2.72 | 7.39 | 20.09 |
 | 1 | 2 | 3 | 4 | 5 |
设偶函数f(x)的定义域为R,当x 时f(x)是增函数,则f(-2),f(
时f(x)是增函数,则f(-2),f( ),f(-3)的大小关系是:( )
),f(-3)的大小关系是:( )
A.f( )>f(-3)>f(-2) )>f(-3)>f(-2) | B.f( )>f(-2)>f(-3) )>f(-2)>f(-3) |
C.f( )<f(-3)<f(-2) )<f(-3)<f(-2) | D.f( )<f(-2)<f(-3) )<f(-2)<f(-3) |
设函数 在
在 上的导函数为
上的导函数为 ,
, 在
在 上的导函数为
上的导函数为 ,若在
,若在 上,
上, 恒成立,则称函数
恒成立,则称函数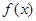 在
在 上为“凸函数”.已知当
上为“凸函数”.已知当 时,
时, 在
在 上是“凸函数”.则
上是“凸函数”.则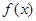 在
在 上 ( )
上 ( )
| A.既有极大值,也有极小值 | B.既有极大值,也有最小值 |
| C.有极大值,没有极小值 | D.没有极大值,也没有极小值 |
函数 的定义域为开区间(a,b),其导函数
的定义域为开区间(a,b),其导函数 在(a,b)内的图像如下图所示,则函数
在(a,b)内的图像如下图所示,则函数 在开区间(a,b)内极小值点的个数有( )
在开区间(a,b)内极小值点的个数有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
 ( )
( )




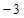


 ,的大致图象是
,的大致图象是