题目内容
椭圆M:
+
=1(a>b>0)的左、右焦点分别为F1,F2,P为椭圆M上任一点,且|PF1•PF2|最大值取值范围为[2c2,3c2]其中c=
,则椭圆M的离心率为 ( )
| x2 |
| a2 |
| y2 |
| b2 |
| a2+b2 |
A、[
| ||||||||
B、[
| ||||||||
C、[
| ||||||||
D、[
|
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:根据题意,|PF1|•|PF2|的最大值为a2,则由题意知2c2≤a2≤3c2,由此能够导出椭圆m的离心率e的取值范围.
解答:
解:∵|PF1|•|PF2|的最大值=a2,
∴由题意知2c2≤a2≤3c2,
∴
c≤a≤
c,
∴
≤
≤
.故椭圆m的离心率e的取值范围[
,
].
故选:B.
∴由题意知2c2≤a2≤3c2,
∴
| 2 |
| 3 |
∴
| ||
| 3 |
| c |
| a |
| ||
| 2 |
| ||
| 3 |
| ||
| 2 |
故选:B.
点评:本题主要考查椭圆的简单性质.考查对基础知识的综合运用.|PF1|•|PF2|的最大值=a2是正确解题的关键.

练习册系列答案
相关题目
光线从点A(-3,5)射到x轴上,经反射以后经过点B(2,10),则光线从A到B的距离为( )
A、5
| ||
B、2
| ||
C、5
| ||
D、10
|
已知函数y=x2-2x+3在[0,a](a>0)上最大值是3,最小值是2,则实数a的范围是( )
| A、0<a<1 |
| B、0<a≤2 |
| C、1≤a≤2 |
| D、0≤a≤2 |
关于x的不等式(mx-1)(x-2)<0的解为2<x<
,则m的取值范围是( )
| 1 |
| m |
A、m<
| ||
| B、m>0 | ||
C、0<m<
| ||
| D、0<m<2 |
若“0≤x≤4”是“(x-a)[x-(a+2)]≤0”的必要不充分条件,则实数a的取值范围是( )
| A、(0,2) |
| B、[0,2] |
| C、[-2,0] |
| D、(-2,0) |
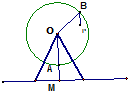 某公园的摩天轮观览车主架示意图如图所示,其中O为轮轴中心,距地面32m(即OM长),巨轮半径为30m,AM=BP=2m,巨轮逆时针旋转且12分钟转动一圈.若点M为P的初始位置(O,A,M共线),经过t分钟,该吊舱P距地面的高度为h(t),则h(t)=
某公园的摩天轮观览车主架示意图如图所示,其中O为轮轴中心,距地面32m(即OM长),巨轮半径为30m,AM=BP=2m,巨轮逆时针旋转且12分钟转动一圈.若点M为P的初始位置(O,A,M共线),经过t分钟,该吊舱P距地面的高度为h(t),则h(t)=