题目内容
13. 如图,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AD=AP=2,AB=2$\sqrt{7}$,E为棱PD中点.
如图,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AD=AP=2,AB=2$\sqrt{7}$,E为棱PD中点.(1)求证:PD⊥平面ABE;
(2)求四棱锥P-ABCD外接球的体积.
分析 (1)推导出PA⊥AB,AB⊥AD,从而AB⊥平面PAD,进而AB⊥PD,再由AE⊥PD,能证明PD⊥平面ABE.
(II)四棱锥P-ABCD外接球球心是线段BD和线段PA的垂直平分线交点O,由此能求出四棱锥P-ABCD外接球的体积.
解答 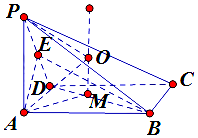 证明:(1)∵PA⊥底面ABCD,AB?底面ABCD,
证明:(1)∵PA⊥底面ABCD,AB?底面ABCD,
∴PA⊥AB,又∵底面ABCD为矩形,
∴AB⊥AD,PA∩AD,
又PA?平面PAD,AD?平面PAD,
∴AB⊥平面PAD,又PD?平面PAD,∴AB⊥PD,AD=AP,E为PD中点,
∴AE⊥PD,AE∩AB=A,AE?平面ABE,AB?平面ABE,
∴PD⊥平面ABE.
解:(II)四棱锥P-ABCD外接球球心是线段BD和线段PA的垂直平分线交点O,
由已知BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=$\sqrt{{2}^{2}+(2\sqrt{7})^{2}}$=4$\sqrt{2}$,
设C为BD中点,∴AM=2$\sqrt{2}$,OM=$\frac{1}{2}$AP=1,
∴OA=$\sqrt{A{M}^{2}+O{M}^{2}}$=$\sqrt{{1}^{2}+(2\sqrt{2})^{2}}$=3,
∴四棱锥P-ABCD外接球的体积是$\frac{4}{3}πA{M}^{3}$=36π.
点评 本题考查线面垂直的证明,考查四棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
8.设a,b均为实数,则“a>b”是“a3>b3”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
18.已知数列{an}满足an+1-an=2,a1=-5,则|a1|+|a2|+…+|a6|=( )
| A. | 9 | B. | 15 | C. | 18 | D. | 30 |
5.设集合A={x|x2-16>0},B={x|-2<x≤6},则A∩B等于( )
| A. | (-2,4) | B. | (4,6] | C. | (-4,6) | D. | (-4,-2) |
2.复数(2+i)i的共轭复数的虚部是( )
| A. | 2 | B. | -2 | C. | 2i | D. | -2i |
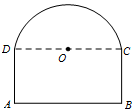 某隧道截面如图,其下部形状是矩形ABCD,上部形状是以CD为直径的半圆.已知隧道的横截面面积为4+π,设半圆的半径OC=x,隧道横截面的周长(即矩形三边长与圆弧长之和)为f(x).
某隧道截面如图,其下部形状是矩形ABCD,上部形状是以CD为直径的半圆.已知隧道的横截面面积为4+π,设半圆的半径OC=x,隧道横截面的周长(即矩形三边长与圆弧长之和)为f(x).