题目内容
设函数f（x）=xtanx，若
且f（x1）＞f（x2），则下列结论中必成立的是
- A.x1＞x2
- B.x12＜x22
- C.x12＞x22
- D.x1＜x2
C
分析：判断出函数为偶函数，再根据函数的单调性进行判断．
解答：容易判断，函数为偶函数，由f（x1）＞f（x2），得f（|x1|）＞f（|x2|），
y′=（xtanx）′=tanx+xsec2x；当x＞0时，y′＞0，函数为增函数，所以|x1|＞|x2|，所以 x12＞x22
故选C．
点评：本题考查了函数的求导以及函数的单调性，属于基础题型．
分析：判断出函数为偶函数，再根据函数的单调性进行判断．
解答：容易判断，函数为偶函数，由f（x1）＞f（x2），得f（|x1|）＞f（|x2|），
y′=（xtanx）′=tanx+xsec2x；当x＞0时，y′＞0，函数为增函数，所以|x1|＞|x2|，所以 x12＞x22
故选C．
点评：本题考查了函数的求导以及函数的单调性，属于基础题型．
练习册系列答案
相关题目
为实数）恒成立，求t的取值范围；
在区间（0，2）上极值点的个数．
，其中向量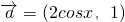
，
．
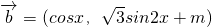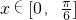时，-4＜f（x）＜4恒成立，求实数m的取值范围．已知表中的对数值有且只有一个是错误的．
| x | 3 | 5 | 6 | 8 | 9 |
| lgx | 2a-b | a+c-1 | 1+a-b-c | 3（1-a-c） | 2（2a-b） |
，则
等于
的图象为
，
满足
，则∠C=
