题目内容
设函数 ,其中向量
,其中向量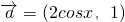 ,
,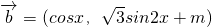 .
.
(Ⅰ)求函数f(x)的最小正周期和在[0,π]上的单调递增区间.
(Ⅱ)当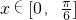 时,-4<f(x)<4恒成立,求实数m的取值范围.
时,-4<f(x)<4恒成立,求实数m的取值范围.
解:(Ⅰ)函数 =2cos2x+
=2cos2x+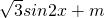 =cos2x+
=cos2x+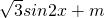 +1=2sin(2x+
+1=2sin(2x+ )+m+1.
)+m+1.
故函数f(x)的最小正周期为 =π.
=π.
令 2kπ- ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,k∈z,可得 kπ-
,k∈z,可得 kπ- ≤x≤kπ+
≤x≤kπ+ ,k∈z,故增区间为[kπ-
,k∈z,故增区间为[kπ- ,kπ+
,kπ+ ],k∈z.
],k∈z.
故在[0,π]上的单调递增区间为[0, ]、[
]、[ ,π].
,π].
(Ⅱ)当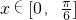 时,
时, ≤2x+
≤2x+ ≤
≤ ,故有
,故有  ≤sin(2x+
≤sin(2x+ )≤1,故 m+2≤f(x)≤m+3.
)≤1,故 m+2≤f(x)≤m+3.
再由-4<f(x)<4恒成立,可得 m+2>-4且 m+3<4,解得-6<m<1,
故实数m的取值范围为(-6,1).
分析:(Ⅰ)滑进函数f(x)的解析式为 2sin(2x+ )+m+1,由此求得周期,令2kπ-
)+m+1,由此求得周期,令2kπ- ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,k∈z,求出函数的单调增区间,即可得到在[0,π]上的单调递增区间.
,k∈z,求出函数的单调增区间,即可得到在[0,π]上的单调递增区间.
(Ⅱ)当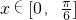 时,求得m+2≤f(x)≤m+3,再由-4<f(x)<4恒成立,可得 m+2>-4且 m+3<4,由此求得实数m的取值范围.
时,求得m+2≤f(x)≤m+3,再由-4<f(x)<4恒成立,可得 m+2>-4且 m+3<4,由此求得实数m的取值范围.
点评:本题主要考查三角函数的恒等变换,三角函数的周期性及其求法,复合三角函数的单调性,函数的恒成立问题,属于中档题.
 =2cos2x+
=2cos2x+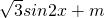 =cos2x+
=cos2x+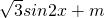 +1=2sin(2x+
+1=2sin(2x+ )+m+1.
)+m+1.故函数f(x)的最小正周期为
 =π.
=π.令 2kπ-
 ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,k∈z,可得 kπ-
,k∈z,可得 kπ- ≤x≤kπ+
≤x≤kπ+ ,k∈z,故增区间为[kπ-
,k∈z,故增区间为[kπ- ,kπ+
,kπ+ ],k∈z.
],k∈z.故在[0,π]上的单调递增区间为[0,
 ]、[
]、[ ,π].
,π].(Ⅱ)当
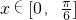 时,
时, ≤2x+
≤2x+ ≤
≤ ,故有
,故有  ≤sin(2x+
≤sin(2x+ )≤1,故 m+2≤f(x)≤m+3.
)≤1,故 m+2≤f(x)≤m+3.再由-4<f(x)<4恒成立,可得 m+2>-4且 m+3<4,解得-6<m<1,
故实数m的取值范围为(-6,1).
分析:(Ⅰ)滑进函数f(x)的解析式为 2sin(2x+
 )+m+1,由此求得周期,令2kπ-
)+m+1,由此求得周期,令2kπ- ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,k∈z,求出函数的单调增区间,即可得到在[0,π]上的单调递增区间.
,k∈z,求出函数的单调增区间,即可得到在[0,π]上的单调递增区间.(Ⅱ)当
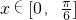 时,求得m+2≤f(x)≤m+3,再由-4<f(x)<4恒成立,可得 m+2>-4且 m+3<4,由此求得实数m的取值范围.
时,求得m+2≤f(x)≤m+3,再由-4<f(x)<4恒成立,可得 m+2>-4且 m+3<4,由此求得实数m的取值范围.点评:本题主要考查三角函数的恒等变换,三角函数的周期性及其求法,复合三角函数的单调性,函数的恒成立问题,属于中档题.

练习册系列答案
相关题目
 ,其中向量
,其中向量 =(m,cos2x),
=(m,cos2x), =(1+sin2x,1),x∈R,且y=f(x)的图象经过点
=(1+sin2x,1),x∈R,且y=f(x)的图象经过点 .
. ,其中向量
,其中向量 =(2cosx,1),
=(2cosx,1), =(cosx,
=(cosx, sin2x),x∈R.
sin2x),x∈R. ,
, =(m,n)(|m|<
=(m,n)(|m|<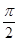 )平移后得到函数y=f(x)的图象,求实数m、n的值.
)平移后得到函数y=f(x)的图象,求实数m、n的值. ,其中向量
,其中向量 ,
, ,
, ,且
,且 的图象经过点
的图象经过点 .(1)求实数
.(1)求实数 的值;
的值; 的最小值及此时
的最小值及此时 值的集合.
值的集合.