题目内容
已知:a>0,b>0,且a+2b=4,则
+
的最小值( )
| 1 |
| a |
| 1 |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:基本不等式
专题:计算题,不等式的解法及应用
分析:
+
=(
+
)•
(a+2b)=
(3+
+
),利用基本不等式可求答案.
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
| 1 |
| 4 |
| 1 |
| 4 |
| 2b |
| a |
| a |
| b |
解答:
解:∵a>0,b>0,且a+2b=4,
∴
+
=(
+
)•
(a+2b)=
(3+
+
)
≥
(3+2
)=
,
当且仅当
=
时取等号,
由
解得
,
∴
+
的最小值是
,
故选A.
∴
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
| 1 |
| 4 |
| 1 |
| 4 |
| 2b |
| a |
| a |
| b |
≥
| 1 |
| 4 |
|
3+2
| ||
| 4 |
当且仅当
| 2b |
| a |
| a |
| b |
由
|
|
∴
| 1 |
| a |
| 1 |
| b |
3+2
| ||
| 4 |
故选A.
点评:该题考查利用基本不等式求函数的最值,已知条件变形后的整体代换是解决该题的关键.

练习册系列答案
相关题目
给出一个算法的程序框图(如图所示),该程序框图的功能是( )
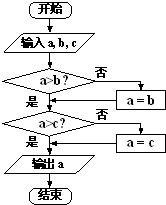

| A、求输出a,b,c三数的最大数 |
| B、求输出a,b,c三数的最小数 |
| C、将a,b,c按从小到大排列 |
| D、将a,b,c按从大到小排列 |
已知在△ABC中,a=
,b=
,B=60°,那么角C等于( )
| 2 |
| 3 |
| A、135° | B、90° |
| C、45° | D、75° |
当a>0时,2a+
的最小值为( )
| 1 |
| a |
| A、3 | ||
B、2
| ||
| C、2 | ||
D、
|
四个同学,争夺三项冠军,冠军获得者可能有的种类是( )
| A、4 |
| B、24 |
| C、43 |
| D、34 |
下列方程中,t为参数.与方程y2=x表示同一曲线的是( )
A、
| |||||||||
B、
| |||||||||
C、
| |||||||||
D、
|
为了得到函数y=sin3x+cos3x的图象,可以将函数y=
sin3x的图象( )
| 2 |
A、向右平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向左平移
|