题目内容
设数列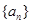 的前
的前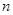 项和为
项和为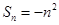 ,数列
,数列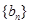 满足:
满足: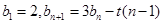 ,已知
,已知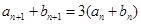 对任意
对任意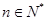 都成立
都成立
(1)求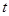 的值
的值
(2)设数列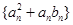 的前
的前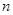 项的和为
项的和为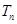 ,问是否存在互不相等的正整数
,问是否存在互不相等的正整数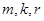 ,使得
,使得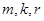 成等差数列,且
成等差数列,且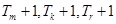 成等比数列?若存在,求出
成等比数列?若存在,求出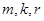 ;若不存在,说明理由
;若不存在,说明理由
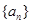 的前
的前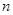 项和为
项和为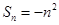 ,数列
,数列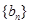 满足:
满足: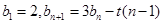 ,已知
,已知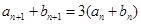 对任意
对任意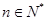 都成立
都成立(1)求
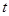 的值
的值(2)设数列
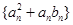 的前
的前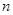 项的和为
项的和为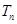 ,问是否存在互不相等的正整数
,问是否存在互不相等的正整数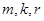 ,使得
,使得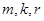 成等差数列,且
成等差数列,且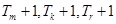 成等比数列?若存在,求出
成等比数列?若存在,求出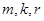 ;若不存在,说明理由
;若不存在,说明理由(1)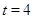 (2)不存在满足条件的正整数m,k,r,使得
(2)不存在满足条件的正整数m,k,r,使得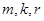 成等差数列,且
成等差数列,且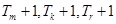 成等比数列.
成等比数列.
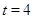 (2)不存在满足条件的正整数m,k,r,使得
(2)不存在满足条件的正整数m,k,r,使得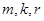 成等差数列,且
成等差数列,且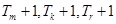 成等比数列.
成等比数列.试题分析:(1)先利用递推关系式
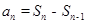 求出数列
求出数列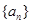 的通项,再利用
的通项,再利用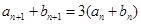 对任意
对任意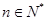 都成立,
都成立,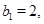 证明出数列
证明出数列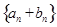 是首项为1,公比为3的等比数列并求出其通项然后
是首项为1,公比为3的等比数列并求出其通项然后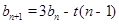
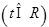 ,所以
,所以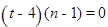 对任意
对任意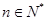 都成立,进而求出t的值;
都成立,进而求出t的值;(2)由(1)得
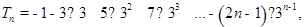 然后利用错位相减法解出
然后利用错位相减法解出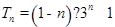
再由
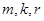 成等差数列,且
成等差数列,且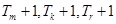 成等比数列.得m=r.这与
成等比数列.得m=r.这与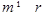 矛盾,所以,不存在满足条件的正整数m,k,r,
矛盾,所以,不存在满足条件的正整数m,k,r,试题解析:(1)当
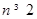 时,
时,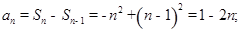
当
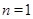 时,
时,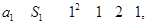 也适合上式.
也适合上式.所以
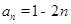 (
(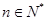 ) .2分
) .2分因为
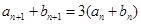 多任意
多任意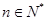 都成立,
都成立,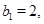
所以
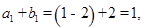
所以
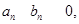 且
且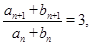
所以数列
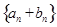 是首项为1,公比为3的等比数列.
是首项为1,公比为3的等比数列.所以
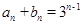 , ..4分
, ..4分即
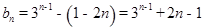
因为
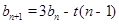
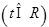 ,
,所以
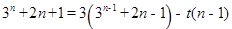
所以
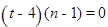 对任意
对任意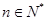 都成立,
都成立,所以
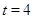 , 6分
, 6分(2)由(1)得
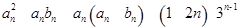 ,
,所以
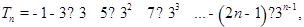
所以
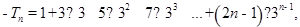
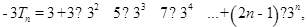
两式相减,得
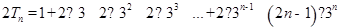
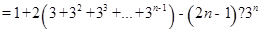
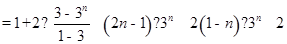
解得
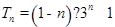 ..8分
..8分若存在互不相等的正整数
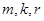 ,使得
,使得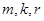 成等差数列,且
成等差数列,且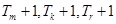 成等比数列.
成等比数列.则
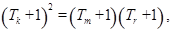
即
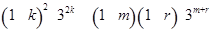 .
.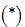
由
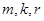 成等差数列,得
成等差数列,得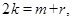 所以
所以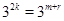 .
.所以由
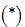 得
得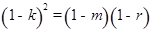 .
.即
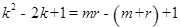
所以
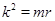
即
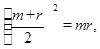 即
即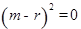 即m=r.
即m=r.这与
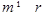 矛盾
矛盾所以,不存在满足条件的正整数m,k,r, .10分

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 中,
中, ,对
,对 总有
总有 成立,
成立, 的值;
的值; ,并用数学归纳法证明
,并用数学归纳法证明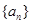 中,已知
中,已知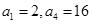 .
.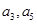 分别为等差数列
分别为等差数列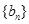 的第3项和第5项,试求数列
的第3项和第5项,试求数列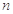 项和
项和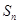 .
.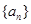 满足
满足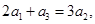 且
且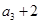 是
是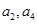 的等差中项
的等差中项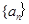 的通项公式;(2)若
的通项公式;(2)若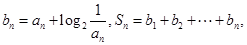 求使
求使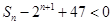 成立的正整数
成立的正整数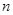 的最小值.
的最小值.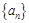 中,
中,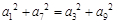 ,记
,记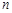 项和为
项和为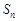 ,其中
,其中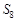
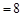 ,则
,则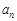 = .
= .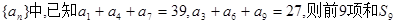 的值为( )
的值为( ) 前项和为
前项和为 ,且点
,且点 在
在 图像上,求
图像上,求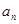
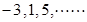 的第15项为( )
的第15项为( ) 中,
中,
 ,则此数列前30项和等于( )
,则此数列前30项和等于( )