题目内容

5．直线y=-x+3与坐标轴围成的三角形的面积是$\frac{9}{2}$．

分析 根据题意，求出直线与两坐标轴的交点坐标，结合三角形面积公式加以计算，即可得到所求三角形的面积．

解答 解：直线y=-x+3，
当x=0时，y=3，当y=0时，x=3，
∴三角形AOB的面积为S=$\frac{1}{2}$×|OA|×|OB|=$\frac{1}{2}$×3×3=$\frac{9}{2}$
即直线y=-x+3与坐标轴围成的三角形的面积是$\frac{9}{2}$
故答案为：$\frac{9}{2}$．

点评 本题给出直线方程，求直线与坐标轴围成三角形的面积．着重考查了直线的方程、三角形面积公式等知识，属于基础题．

练习册系列答案
相关题目
15．已知f（x）是R上的奇函数，其图象与x轴有5个交点，则f（x）=0的所有根之和为0．
16．向量$\overrightarrow{a}$=（2，-3），$\overrightarrow{b}$=（5，-4），则$\overrightarrow{a}$•$\overrightarrow{b}$=（　　）
A．22B．7C．-2D．-15
13．函数y=$\sqrt{3}$sin2x+cos2（x+$\frac{π}{4}$）的振幅为$\sqrt{3}$-1．
20．已知直线l的倾斜角是120°，则这条直线的一个法向量为（　　）
A．（1，$\sqrt{3}$）B．（1，-$\sqrt{3}$）C．（$\sqrt{3}$，1）D．（-$\sqrt{3}$，1）
10．在平面直角坐标系xoy中，已知以O为圆心的圆与直线l：y=mx+（3-4m）（m∈R）恒有公共点，且要求使圆O的面积最小．
（1）求证：直线l过定点，并指出定点坐标；
（2）写出圆O的方程；
（3）圆O与x轴相交于A，B两点，圆内动点P使$\overrightarrow{PO}$2=|$\overrightarrow{PA}$|•|$\overrightarrow{PB}$|，求$\overrightarrow{PA}$•$\overrightarrow{PB}$的取值范围．
17．已知tan（α+β）=$\frac{3}{4}$，tan（β-$\frac{π}{4}$）=$\frac{1}{4}$，那么tan（α+$\frac{π}{4}$）=（　　）
A．$\frac{16}{19}$B．$\frac{16}{13}$C．$\frac{13}{16}$D．$\frac{8}{19}$
14．函数y=sin（2x+$\frac{π}{6}$）sin（2x+$\frac{2π}{3}$）的最小正周期为（　　）
A．$\frac{π}{2}$B．$\frac{π}{4}$C．2πD．π
15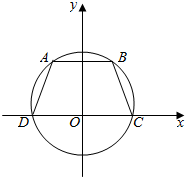．如图，已知等腰梯形ABCD的底边长分别为2和14，腰长为10，则这个等腰梯形的外接圆E的方程为（　　）
A．x2+（y-2）2=53B．x2+（y-2）2=64C．x2+（y-1）2=50D．x2+（x-1）2=64

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网