题目内容
5．在区间[-1，1]上随机取一个数k，使直线$y=kx+\frac{{\sqrt{5}}}{2}$与圆x2+y2=1相交的概率为（ ）| A． | $\frac{3}{4}$ | B． | $\frac{2}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{1}{3}$ |
分析 利用圆心到直线的距离小于等于半径可得到直线与圆有公共点，求出满足条件的k，根据几何概型的概率公式计算即可．
解答 解：要使直线$y=kx+\frac{{\sqrt{5}}}{2}$与圆x2+y2=1相交，
应满足$\frac{\frac{\sqrt{5}}{2}}{\sqrt{{k}^{2}+1}}$＜1，
解得-$\frac{1}{2}$≤k≤$\frac{1}{2}$，
所以在区间[-1，1]上随机取一个数k，
使直线$y=kx+\frac{{\sqrt{5}}}{2}$与圆x2+y2=1相交的概率为P=$\frac{\frac{1}{2}+\frac{1}{2}}{1+1}$=$\frac{1}{2}$．
故选：C．
点评 本题主要考查了几何概型的概率，以及直线与圆相交的性质问题，是基础题目．
练习册系列答案
课堂全解字词句段篇章系列答案
相关题目
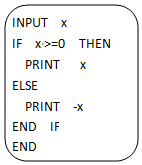当输入的x 值为-5时，如图的程序运行的结果等于5．
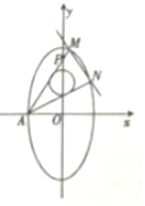已知在平面直角坐标系xOy中，椭圆$C：\frac{y^2}{a^2}+\frac{x^2}{b^2}=1（{a＞b＞0}）$的离心率为$\frac{{\sqrt{3}}}{2}$，A是椭圆的左顶点，M，N是椭圆上的两个动点，直线AM交y轴于点P．
20．若集合A={x|x≥0}，且A∩B=B，则集合B可能是（ ）
| A． | {x|x≥2} | B． | {x|x≤1} | C． | {x|x≥-1} | D． | R |