题目内容
在R上可导的函数f(x)=
x3+
ax2+2bx+c,当x∈(0,1)时取得极大值,当x∈(1,2)时取得极小值,则
的取值范围是( )
| 1 |
| 3 |
| 1 |
| 2 |
| b-4 |
| a-3 |
A、(-
| ||||
B、(-
| ||||
C、(
| ||||
D、(
|
考点:利用导数研究函数的极值
专题:计算题,导数的概念及应用
分析:据极大值点左边导数为正右边导数为负,极小值点左边导数为负右边导数为正得a,b的约束条件,据线性规划求出最值.
解答:
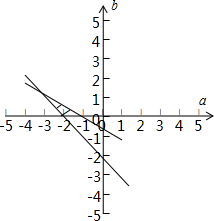 解:∵f(x)=
解:∵f(x)=
x3+
ax2+2bx+c,∴f′(x)=x2+ax+2b
∵函数f(x)在区间(0,1]内取得极大值,在区间(1,2]内取得极小值
∴f′(x)=x2+ax+2b=0在(0,1]和(1,2]内各有一个根
f′(0)>0,f′(1)≤0,f′(2)≥0
即
,区域的三个顶点坐标为(-2,0),(-1,0),(-3,1),
表示点A(3,4)与可行域内的点B连线的斜率,
当(-1,0)时,
最大,最大为1;
当(-3,1)时,
最小,最小为
.
故选:D.
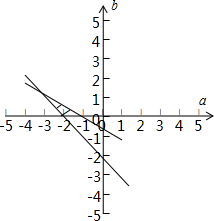 解:∵f(x)=
解:∵f(x)=| 1 |
| 3 |
| 1 |
| 2 |
∵函数f(x)在区间(0,1]内取得极大值,在区间(1,2]内取得极小值
∴f′(x)=x2+ax+2b=0在(0,1]和(1,2]内各有一个根
f′(0)>0,f′(1)≤0,f′(2)≥0
即
|
| b-4 |
| a-3 |
当(-1,0)时,
| b-4 |
| a-3 |
当(-3,1)时,
| b-4 |
| a-3 |
| 1 |
| 2 |
故选:D.
点评:考查学生利用导数研究函数极值的能力,以及会进行简单的线性规划的能力.

练习册系列答案
相关题目
若不等式组
的解集中所含整数解只有-2,求k的取值范围( )
|
| A、[-3,2) |
| B、[-1,2) |
| C、[0,2) |
| D、[1,2) |
在下列命题中,真命题是( )
| A、“若x=3,则x2=9”的逆命题 |
| B、“x=1时,x2-3x+2=0”的否命题 |
| C、若a>b,则ac2>bc2 |
| D、“相似三角形的对应角相等”的逆否命题 |
已知函数f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,0<φ<2π)图象上的一个最高点是(2,
),由这个最高点到相邻的最低点图象与x轴的交点为(6,0),则f(x)=( )
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知函数f(x)=-|x|,则f(x)是( )
| A、奇函数 |
| B、偶函数 |
| C、既是奇函数又是偶函数 |
| D、非奇函数非偶函数 |