Question

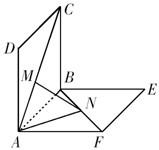如图所示，正方形ABCD和正方形ABEF所在平面互相垂直，且它们的边长都是1，点M在AC上，点N在BF上，若CM=2BN=a(0＜a＜

2

)．
（1）求MN的长；
（2）当a为何值时，MN最小，并求出最小值？
（3）当MN最小时，求三棱锥M-ANB的体积．

Answer 1

分析：（1）由垂直关系可以建立空间直角坐标系，用a表示点M，N的坐标，再由两点间的距离公式可求MN的长；
（2）由（1）中MN的函数表达式，容易求出MN最小时a的值；
（3）由作图知，MP是三棱锥M-ABN底面ABN上的高，由棱锥的体积公式可求出体积．

解答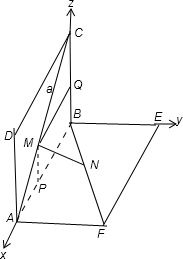：解：（1）如图，建立平面直角坐标系；               
∵正方形的边长为1，
则A（1，0，0），B（0，0，0），C（0，0，1），E（0，1，0），F（1，1，0），
由CM=2BN=a(0＜a＜

2

)，在平面ABCD内作MQ⊥BC，MP⊥AB，垂足分别为Q，P，
则CQ=MQ=

a

2

，MP=1-

a

2

，
∴M（

a

2

，0，1-

a

2

），N（

a

2 2

，

a

2 2

，0）；
∴MN=

( a 2 - a 2 2 ) 2+(0- a 2 2 )2+(1- a 2 2 )2

=

1

2

3(a- 2 2 3 )2+ 4 3

；

（2）由（1）知，当a=

2 2

3

时，MN有最小值，此时MN=

1

2

•

4 3

=

3

3

；

（3）在平面ABCD内，MP⊥AB，且平面ABCD⊥平面ABEF，
∴MP⊥平面ABEF；
所以，三棱锥M-ABN的体积为：V=

1

3

•S_△ABN•h
=

1

3

•

1

2

•AB•BN•sin45°•MP
=

1

3

•

1

2

•1•

a

2

•

2

2

•(1-

a

2

)
=

2 a

24

(1-

a

2

)
=

2

24

•

2 2

3

(1-

1

2

•

2 2

3

)
=

1

54

．

点评：本题综合考查了空间直角坐标系的应用，求两点间的距离，函数的最大值，三棱锥的体积等，根据垂直关系建立空间直角坐标系是解本题的关键．