题目内容
已知函数
(1)若直线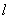 过点
过点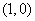 ,并且与曲线
,并且与曲线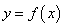 相切,求直线
相切,求直线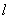 的方程;
的方程;
(2)设函数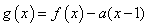 在
在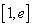 上有且只有一个零点,求
上有且只有一个零点,求 的取值范围。
的取值范围。
(其中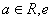 为自然对数的底数)
为自然对数的底数)
解:(1)设切点坐标为 ,则
,则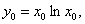 切线的斜率为
切线的斜率为
所以切线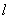 的方程为
的方程为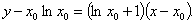 ………………2分
………………2分
又切线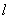 过点(1,0),所以有
过点(1,0),所以有
即 解得
解得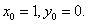
所以直线 的方程为
的方程为
(或:设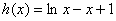 ,则
,则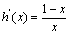
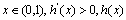 单增,
单增,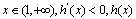 单减
单减
 有唯一解,
有唯一解,
所以直线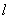 的方程为
的方程为
(2)因为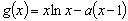 ,注意到g(1)=0
,注意到g(1)=0
所以,所求问题等价于函数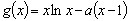 在
在 上没有零点.
上没有零点.
因为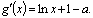
所以由 <0
<0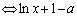 <0
<0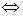 0<
0<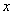 <
< >0
>0 >
>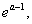
所以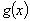 在
在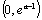 上单调递减,在
上单调递减,在 上单调递增.
上单调递增.
①当 即
即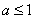 时,
时,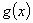 在
在 上单调递增,所以
上单调递增,所以 >
>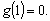
此时函数g(x)在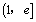 上没有零点
上没有零点
②当1<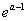 <e,即1<a<2时,
<e,即1<a<2时,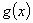 在
在 上单调递减,在
上单调递减,在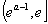 上单调递增.
上单调递增.
又因为g(1)=0,g(e)=e-ae+a,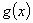 在
在 上的最小值为
上的最小值为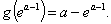
所以,(i)当1<a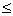
 时,
时,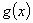 在
在 上的最大值g(e)
上的最大值g(e)  0,即此时函数g(x)在
0,即此时函数g(x)在 上有零点。 (ii)当
上有零点。 (ii)当 <a<2时, g(e) <0,即此时函数g(x)在
<a<2时, g(e) <0,即此时函数g(x)在 上没有零点.…10分
上没有零点.…10分
③当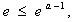 即
即 时,
时,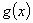 在
在 上单调递减,所以
上单调递减,所以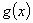 在
在 上满足
上满足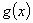 <
< 此时函数g(x)在
此时函数g(x)在 上没有零点
上没有零点
综上,所求的a的取值范围是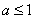 或
或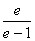 <a
<a

练习册系列答案
相关题目
 互相平行,其中
互相平行,其中 .
. 和
和 的值;
的值; ,求
,求 的值.
的值. 在(0,1)内有极上值,则实数b的取值范围是__________.
在(0,1)内有极上值,则实数b的取值范围是__________. ,则它们的图象可能是( )
,则它们的图象可能是( )
 中,内角
中,内角 所对的边分别为
所对的边分别为 ,且
,且 。
。 ;
; ,求
,求 (A) 16
(A) 16 (B)
(B)  (C) 4 (D)
(C) 4 (D) 
 ,则
,则 = ( )
= ( ) B.
B. C.2015 D. 2014
C.2015 D. 2014