题目内容
 若在x∈[0,
若在x∈[0,| π |
| 2 |
| 3 |
分析:把已知等式左边提取2后,利用特殊角的三角函数值及两角和与差的正弦函数公式化为一个角的正弦函数,由x的范围求出这个角的范围,画出此时正弦函数的图象,根据函数值y对应的x有两个不同的值,由图象得出满足题意的正弦函数的值域,列出关于k的不等式,求出不等式的解集即可得到k的取值范围.
解答:解:cos2x+
sin2x=k+1,
得2(
cos2x+
sin2x)=k+1,即2sin(2x+
)=k+1,
可得:sin(2x+
)=
,
由0≤x≤
,得
≤2x+
≤
,
∵y=sin(2x+
)在x∈[0,
]上的图象形状如图,
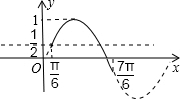
∴当
≤
<1时,方程有两个不同的根,
解得:0≤k<1.
答案:D
| 3 |
得2(
| 1 |
| 2 |
| ||
| 2 |
| π |
| 6 |
可得:sin(2x+
| π |
| 6 |
| k+1 |
| 2 |
由0≤x≤
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
∵y=sin(2x+
| π |
| 6 |
| π |
| 2 |

∴当
| 1 |
| 2 |
| k+1 |
| 2 |
解得:0≤k<1.
答案:D
点评:此题考查了两角和与差的正弦函数公式,正弦函数的图象与性质,以及正弦函数的定义域与值域,利用了数形结合的思想,解题的思路为:利用三角函数的恒等变形把已知等式的左边化为一个正弦函数,利用正弦函数的图象与性质来解决问题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目