题目内容
 某造纸厂拟建一座平面图形为矩形且面积为162平方米的三级污水处理池,池的深度一定(平面图形如图所示),如果池四周围墙建造单价为400元/米,中间两道隔墙建造单价为248元/米,池底建造单价为80元/米2,水池所有墙的厚度忽略不计,试设计污水处理池的长与宽,使总造价最低,并求出最低总造价.
某造纸厂拟建一座平面图形为矩形且面积为162平方米的三级污水处理池,池的深度一定(平面图形如图所示),如果池四周围墙建造单价为400元/米,中间两道隔墙建造单价为248元/米,池底建造单价为80元/米2,水池所有墙的厚度忽略不计,试设计污水处理池的长与宽,使总造价最低,并求出最低总造价.
【答案】分析:污水处理池的底面积一定,设宽为x米,可表示出长,从而得出总造价f(x),利用基本不等式求出最小值即可.
解答:解:设污水处理池的宽为x米,则长为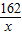 米.
米.
则总造价f(x)=400×(2x+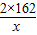 )+248×2x+80×162=1296x+
)+248×2x+80×162=1296x+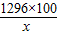 +12960
+12960
=1296(x+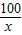 )+12960≥1296×2×
)+12960≥1296×2×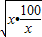 +12960=38880(元),
+12960=38880(元),
当且仅当x=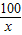 (x>0),即x=10时,取等号.
(x>0),即x=10时,取等号.
∴当长为16.2米,宽为10米时总造价最低,最低总造价为38880元.
点评:本题主要考查了建立函数解析式,利用基本不等式求函数最值的能力,同时考查了运算求解能力,属于中档题.
解答:解:设污水处理池的宽为x米,则长为
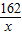 米.
米.则总造价f(x)=400×(2x+
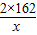 )+248×2x+80×162=1296x+
)+248×2x+80×162=1296x+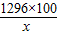 +12960
+12960=1296(x+
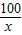 )+12960≥1296×2×
)+12960≥1296×2×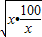 +12960=38880(元),
+12960=38880(元),当且仅当x=
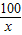 (x>0),即x=10时,取等号.
(x>0),即x=10时,取等号.∴当长为16.2米,宽为10米时总造价最低,最低总造价为38880元.
点评:本题主要考查了建立函数解析式,利用基本不等式求函数最值的能力,同时考查了运算求解能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 某造纸厂拟建一座平面图形为矩形且面积为162平方米的三级污水处理池,池的深度一定(平面图如图所示),如果池四周围墙建造单价为400元/米,中间两道隔墙建造单价为248元/米,池底建造单价为80
某造纸厂拟建一座平面图形为矩形且面积为162平方米的三级污水处理池,池的深度一定(平面图如图所示),如果池四周围墙建造单价为400元/米,中间两道隔墙建造单价为248元/米,池底建造单价为80 某造纸厂拟建一座平面图形为矩形且面积为162平方米的三级污水处理池,池的深度一定(平面图形如图所示),如果池四周围墙建造单价为400元/米,中间两道隔墙建造单价为248元/米,池底建造单价为80元/米2,水池所有墙的厚度忽略不计,试设计污水处理池的长与宽,使总造价最低,并求出最低总造价.
某造纸厂拟建一座平面图形为矩形且面积为162平方米的三级污水处理池,池的深度一定(平面图形如图所示),如果池四周围墙建造单价为400元/米,中间两道隔墙建造单价为248元/米,池底建造单价为80元/米2,水池所有墙的厚度忽略不计,试设计污水处理池的长与宽,使总造价最低,并求出最低总造价. 某造纸厂拟建一座平面图形为矩形且面积为162平方米的三级污水处理池,池的深度一定(平面图如图所示),如果池四周围墙建造单价为400元/米,中间两道隔墙建造单价为248元/米,池底建造单价为80元/米2,水池所有墙的厚度忽略不计.
某造纸厂拟建一座平面图形为矩形且面积为162平方米的三级污水处理池,池的深度一定(平面图如图所示),如果池四周围墙建造单价为400元/米,中间两道隔墙建造单价为248元/米,池底建造单价为80元/米2,水池所有墙的厚度忽略不计.