题目内容
已知数列 满足:
满足: (
( ).
).
(1)求 的值;
的值;
(2)求证:数列 是等比数列;
是等比数列;
(3)令 ,
, ,如果对任意
,如果对任意 ,都有
,都有 ,
,
求实数 的取值范围.
的取值范围.
(1)
(2)根据等比数列的定义只要证明从第二项起,每一项与前一项的比值为定值即可。
(3)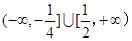
解析试题分析:解:(I) 3分
3分
(II)由题可知: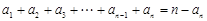 ①
① ②
②
②-①可得 ..5分
..5分
即: ,又
,又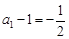 7分
7分
所以数列 是以
是以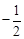 为首项,以
为首项,以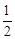 为公比的等比数列 8分
为公比的等比数列 8分
(Ⅲ)由(2)可得 , 9分
, 9分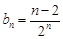 10分
10分
由 可得
可得
由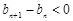 可得
可得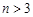 11分
11分
所以 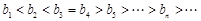
故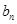 有最大值
有最大值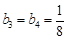
所以,对任意 ,有
,有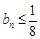 13分
13分
如果对任意 ,都有
,都有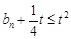 ,即
,即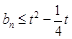 成立,
成立,
则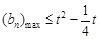 ,故有:
,故有: , 15分
, 15分
解得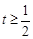 或
或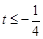
所以,实数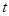 的取值范围是
的取值范围是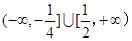 16
16
考点:等比数列
点评:解决的关键是根据数列的定义,以及不等式来综合运用,属于中档题。

练习册系列答案
相关题目
 是各项均不为0的等差数列,公差为
是各项均不为0的等差数列,公差为 ,
, 为其前n项和,且满足
为其前n项和,且满足 ,
, .数列
.数列 满足
满足 ,
, 为数列
为数列 项和.
项和. 的通项公式
的通项公式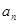 ;
;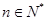 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,使得
,使得 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有
 ,求n的值;
,求n的值; }是公比为q(q≠﹣1)的等比数列,a为常数,求证:数列{an}为等比数列的充要条件为
}是公比为q(q≠﹣1)的等比数列,a为常数,求证:数列{an}为等比数列的充要条件为
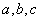 都是正数,且
都是正数,且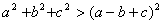
 中,
中, ,公比
,公比 .
. 为
为
 ,求数列
,求数列 的通项公式.
的通项公式.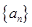 满足:
满足: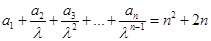 (其中常数
(其中常数 ).
). 时,数列
时,数列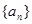 中,
中,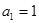 ,且
,且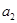 是
是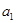 和
和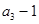 的等差中项.
的等差中项.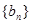 满足
满足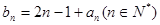 ,求
,求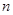 项和
项和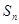 .
.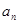 }是等差数列,且满足:a1+a2+a3=6,a5=5;
}是等差数列,且满足:a1+a2+a3=6,a5=5;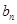 }满足:
}满足: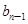 =
=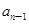 (n≥2,n∈N﹡),b1=1.
(n≥2,n∈N﹡),b1=1.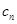 =
=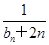 (n∈N﹡),若{
(n∈N﹡),若{ ,求
,求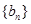 满足
满足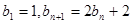 ,
,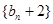 为等比数列 (2)求数列
为等比数列 (2)求数列