题目内容
规定符号“*”表示一种两个正实数之间的运算，即a*b=
+a+b，a，b是正实数，已知3*k=6，则函数f（x）=k*x的值域是 ．
| a+b |
考点：函数的值域
专题：函数的性质及应用
分析：根据新定义先求出k的值，然后求出函数f（x）的表达式，再求其值域即可得出答案．
解答：
解：∵a*b=
+a+b，
∴3*k=
+3+k=6，
解得k=1或k=6，
经检验知k=6不符合题意，
∴k=1，
∴f（x）=k*x=1*x=
+1+x，∵x＞0，
∴f（x）的值域为：（2，+∞），
故答案为：（2，+∞）．
| a+b |
∴3*k=
| 3+k |
解得k=1或k=6，
经检验知k=6不符合题意，
∴k=1，
∴f（x）=k*x=1*x=
| 1+x |
∴f（x）的值域为：（2，+∞），
故答案为：（2，+∞）．
点评：本题考查了函数的值域，难度适中，关键是对新定义的理解与把握．
练习册系列答案
名校课堂系列答案
相关题目
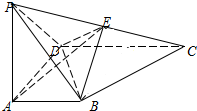如图，在四棱锥P-ABCD中，AD=CD=2AB=2，PA⊥AD，AB∥CD，CD⊥AD，E为PC的中点，且DE=EC．