题目内容
17.若p:x<-1,q:x<-4,则?p是?q的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 根据集合的包含关系以及充分必要条件的定义判断p,q的关系,再根据互逆命题的关系判断即可.
解答 解:若p:x<-1,q:x<-4,
则q是p的充分不必要条件,
即?p是?q的充分不必要条件,
故选:A.
点评 本题考查了充分必要条件,考查集合的包含关系以及互逆命题的关系,是一道基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.已知α为锐角,且$sinα=\frac{4}{5}$,则cos(π-α)=( )
| A. | $-\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | $-\frac{4}{5}$ | D. | $\frac{4}{5}$ |
12.如果点P在平面区域$\left\{{\begin{array}{l}{x≥1}\\{y≤2}\\{x≤y}\end{array}}\right.$上,点M的坐标为(3,0),那么|PM|的最小值是( )
| A. | $\sqrt{5}$ | B. | $\sqrt{2}$ | C. | $\frac{3}{2}\sqrt{2}$ | D. | $2\sqrt{2}$ |
2.已知抛物线y2=4x的焦点F与椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的一个焦点重合,它们在第一象限内的交点为P,且PF与x轴垂直,则椭圆的离心率为( )
| A. | $\sqrt{3}-\sqrt{2}$ | B. | $\sqrt{2}-1$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
4.已知函数f(x)=$\left\{\begin{array}{l}{x+1,x≤0}\\{lo{g}_{2}x,x>0}\end{array}\right.$,则函数y=f[f(x)]-1的零点个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
2.若圆x2+y2-2x-2y=0上至少有三个不同点到直线l:y=kx的距离为$\frac{{\sqrt{2}}}{2}$,则直线l的倾斜角的取值范围是( )
| A. | [15°,45°] | B. | [15°,75°] | C. | [30°,60°] | D. | [0°,90°] |
 如图,在直三棱柱ABC-A1B1C1中,AB=$\sqrt{3},BC=1,A{A_1}$=AC=2,E,F分别为A1C1,BC的中点.
如图,在直三棱柱ABC-A1B1C1中,AB=$\sqrt{3},BC=1,A{A_1}$=AC=2,E,F分别为A1C1,BC的中点.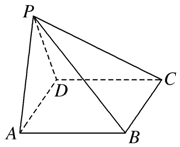 如图,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,$AB=\sqrt{3}$,BC=1,PA=2,E为PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,$AB=\sqrt{3}$,BC=1,PA=2,E为PD的中点.