题目内容
12.如果点P在平面区域$\left\{{\begin{array}{l}{x≥1}\\{y≤2}\\{x≤y}\end{array}}\right.$上,点M的坐标为(3,0),那么|PM|的最小值是( )| A. | $\sqrt{5}$ | B. | $\sqrt{2}$ | C. | $\frac{3}{2}\sqrt{2}$ | D. | $2\sqrt{2}$ |
分析 由约束条件作出可行域,再由点到直线的距离公式求出|PM|的最小值.
解答 解:由约束条件$\left\{{\begin{array}{l}{x≥1}\\{y≤2}\\{x≤y}\end{array}}\right.$作出可行域如图,
由图可知,|PM|的最小值为M(3,0)到直线x-y=0的距离,等于$\frac{|3|}{\sqrt{2}}=\frac{3\sqrt{2}}{2}$.
故选:C.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
20.已知全集U={0,1,2,3,4},集合A={1,2,3},B={2,4},则A∩(∁UB)为( )
| A. | {0,1,3} | B. | {1,3} | C. | {0,2,4} | D. | {0,2,3,4} |
7.如图所示的流程图,若输入x的值为0,则输出x的值为( )


| A. | 2016 | B. | 2016.5 | C. | 2019 | D. | 2017.5 |
17.若p:x<-1,q:x<-4,则?p是?q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
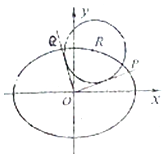 如图,在平面直角坐标系xOy中,已知R(x0,y0)是椭圆C:$\frac{x^2}{24}+\frac{y^2}{12}$=1上的一点,从原点O向圆R:(x-x0)2+(y-y0)2=8作两条切线,分别交椭圆于P,Q两点.
如图,在平面直角坐标系xOy中,已知R(x0,y0)是椭圆C:$\frac{x^2}{24}+\frac{y^2}{12}$=1上的一点,从原点O向圆R:(x-x0)2+(y-y0)2=8作两条切线,分别交椭圆于P,Q两点.