题目内容
14.设n∈N*,数列{an}满足a2+a3=8,an+1=an+2.(I)求数列{an}的通项公式;
(Ⅱ)设bn=$\frac{1}{{a}_{n}•{a}_{n+2}}$,求数列{bn}的前n项和Tn.
分析 (1)利用等差数列的通项公式即可得出;
(2)利用“裂项求和”即可得出.
解答 解:(1)an+1-an=2,
∴$\left\{\begin{array}{l}{{a}_{3}-{a}_{2}=2}\\{{a}_{3}+{a}_{2}=8}\end{array}\right.$,解得:a3=5,a2=3,a1=1
数列{an}是1为首项,以2为公差的等差数列,
an=2n-1,
(2)bn=$\frac{1}{{a}_{n}•{a}_{n+2}}$=$\frac{1}{(2n-1)(2n+3)}$=$\frac{1}{4}$($\frac{1}{2n-1}$-$\frac{1}{2n+3}$),
数列{bn}的前n项和Tn,Tn=$\frac{1}{4}$[(1-$\frac{1}{5}$)+($\frac{1}{3}$-$\frac{1}{7}$)+($\frac{1}{5}$-$\frac{1}{9}$)+…+($\frac{1}{2n-1}$-$\frac{1}{2n+3}$)]
=$\frac{1}{4}$(1+$\frac{1}{3}$-$\frac{1}{2n+1}$-$\frac{1}{2n+3}$),
=$\frac{4{n}^{2}+5n}{3(2n+1)(2n+3)}$.
点评 本题考查了等差数列的通项公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
5.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,过点F的直线与椭圆交于点A,B,若AB中点为(1,-$\frac{1}{2}$),且直线AB的倾斜角为45°,则椭圆方程为( )
| A. | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1 | B. | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1 | C. | $\frac{2{x}^{2}}{9}$+$\frac{4{y}^{2}}{9}$=1 | D. | $\frac{{x}^{2}}{9}$+$\frac{2{y}^{2}}{9}$=1 |
6.从5人中选3人参加座谈会,其中甲必须参加,则不同的选法有( )
| A. | 12种 | B. | 6种 | C. | 5种 | D. | 4种 |
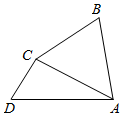 如图四边形ABCD,a,b,c为△ABC的内角A,B,C的对边,且满足b(1+cosA)=a(2-cosB).
如图四边形ABCD,a,b,c为△ABC的内角A,B,C的对边,且满足b(1+cosA)=a(2-cosB).