题目内容
已知a>1,λ>0,求证:loga(a+λ)>loga+λ(a+2λ).
证明:loga(a+λ)-log(a+λ)(a+2λ)
=![]() -
-![]()
=![]() .
.
∵a>1,λ>0,
∴lga>0,lg(a+2λ)>0,且lga≠lg(a+2λ).
∴lga·lg(a+2λ)<[![]() ]2=[
]2=[![]() ]2<[
]2<[![]() ]2
]2
=lg2(a+λ).
∴![]() >0.
>0.
∴loga(a+λ)>log(a+λ)(a+2λ).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
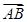 +
+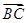 =
=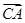 ;
;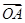 +
+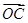 =
=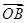 ;
;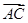 =
=