题目内容
已知椭圆 ,过椭圆左顶点A(-a,0)的直线L与椭圆交于Q,与y轴交于R,过原点与L平行的直线与椭圆交于P,求证:AQ,
,过椭圆左顶点A(-a,0)的直线L与椭圆交于Q,与y轴交于R,过原点与L平行的直线与椭圆交于P,求证:AQ, ,AR成等比数列.
,AR成等比数列.
【答案】分析:根据题意设过左顶点的直线解析式为:y-0=k(x+a)则与L平行的直线为y=kx分别求出Q、R、P点坐标,表示出AQ, OP,AR.只需证2OP2=AQ•AR即可得证.
OP,AR.只需证2OP2=AQ•AR即可得证.
解答:解:设过左顶点A的直线L解析式为:y-0=k(x+a)即y=kx+ka,与y轴交点R坐标为(0,ka);
AR= ;
;
联立
得到AQ=2 ;
;
则过原点的直线为y=kx,与椭圆的交点为P,
联立
得:
所以P( ,k
,k ),OP=
),OP= .
.
得:2OP2=AQ•AR
故AQ, ,AR成等比数列.
,AR成等比数列.
点评:考查学生运用等比数列性质的能力,以及应用椭圆性质的能力.
 OP,AR.只需证2OP2=AQ•AR即可得证.
OP,AR.只需证2OP2=AQ•AR即可得证.解答:解:设过左顶点A的直线L解析式为:y-0=k(x+a)即y=kx+ka,与y轴交点R坐标为(0,ka);
AR=
 ;
;联立

得到AQ=2
 ;
;则过原点的直线为y=kx,与椭圆的交点为P,
联立

得:

所以P(
 ,k
,k ),OP=
),OP= .
.得:2OP2=AQ•AR
故AQ,
 ,AR成等比数列.
,AR成等比数列.点评:考查学生运用等比数列性质的能力,以及应用椭圆性质的能力.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
 上不同于左顶点A、右顶点B的任意一点,记直线PA,PB的斜率分别为k1,k2,则k1•k2的值为 .
上不同于左顶点A、右顶点B的任意一点,记直线PA,PB的斜率分别为k1,k2,则k1•k2的值为 .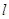 :
: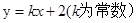 过椭圆
过椭圆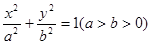 的上顶点B和左焦点F,且被圆
的上顶点B和左焦点F,且被圆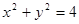 截得的弦长为
截得的弦长为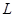 ,若
,若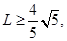 则椭圆离心率
则椭圆离心率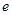 的取值范围是( )
的取值范围是( )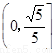
 B.
B.
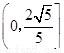 C.
C.
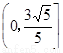 D.
D.
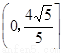
 =1左焦点F1的弦,且
=1左焦点F1的弦,且 ,其中
,其中 是椭圆的右焦点,则弦AB的长是_______
是椭圆的右焦点,则弦AB的长是_______